题目内容
①定义在R上函数f(x)满足f(2)>f(1),则f(x)是R上的增函数;
②定义在R上函数f(x)满足f(2)>f(1),则f(x)在R上不是减函数;
③定义在R上函数f(x)在(-∞,0]是增函数,在[0,+∞)上也是增函数,则f(x)在R上单调递增;
④定义在R上函数f(x)在(-∞,0)是增函数,在[0,+∞)上也是增函数,则f(x)在R上单调递增;
以上说法正确的( )
②定义在R上函数f(x)满足f(2)>f(1),则f(x)在R上不是减函数;
③定义在R上函数f(x)在(-∞,0]是增函数,在[0,+∞)上也是增函数,则f(x)在R上单调递增;
④定义在R上函数f(x)在(-∞,0)是增函数,在[0,+∞)上也是增函数,则f(x)在R上单调递增;
以上说法正确的( )
| A、②③ | B、②④ | C、③④ | D、②③④ |
考点:命题的真假判断与应用
专题:函数的性质及应用
分析:①,举例说明,f(x)=|x|,满足f(2)>f(1),但f(x)在(-∞,0]上递减,在[0,+∞)上是递增函数,可判断①;
②,利用反证法,假设f(x)在R上是减函数,导出矛盾,可判断②;
③,利用函数单调性的定义可判断③;
④,依题意,作图,数形结合可判断④
②,利用反证法,假设f(x)在R上是减函数,导出矛盾,可判断②;
③,利用函数单调性的定义可判断③;
④,依题意,作图,数形结合可判断④
解答:
解:对于①,定义在R上函数f(x)满足f(2)>f(1),则f(x)是R上的增函数,错误.
如f(x)=|x|,满足f(2)>f(1),但f(x)在(-∞,0]上递减,在[0,+∞)上是递增函数;
对于②,假设f(x)在R上是减函数,则f(2)<f(1),与f(x)满足f(2)>f(1)矛盾,故假设错误,原命题正确,即②正确;
对于③,定义在R上函数f(x)在(-∞,0]是增函数,在[0,+∞)上也是增函数,则f(x)在R上单调递增,故③正确;
对于④,定义在R上函数f(x)在(-∞,0)是增函数,在[0,+∞)上也是增函数,则f(x)在R上不一定单调递增,
如图:
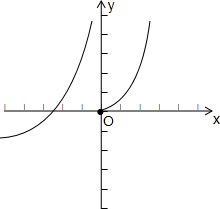
故④错误;
故选:A.
如f(x)=|x|,满足f(2)>f(1),但f(x)在(-∞,0]上递减,在[0,+∞)上是递增函数;
对于②,假设f(x)在R上是减函数,则f(2)<f(1),与f(x)满足f(2)>f(1)矛盾,故假设错误,原命题正确,即②正确;
对于③,定义在R上函数f(x)在(-∞,0]是增函数,在[0,+∞)上也是增函数,则f(x)在R上单调递增,故③正确;
对于④,定义在R上函数f(x)在(-∞,0)是增函数,在[0,+∞)上也是增函数,则f(x)在R上不一定单调递增,
如图:
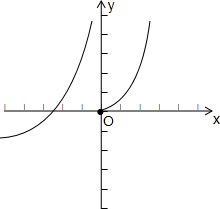
故④错误;
故选:A.
点评:本题考查命题的真假判断与应用,着重考查函数的单调性,考查分析、推理与作图能力,是中档题.

练习册系列答案
 名师导航单元期末冲刺100分系列答案
名师导航单元期末冲刺100分系列答案 名校名卷单元同步训练测试题系列答案
名校名卷单元同步训练测试题系列答案
相关题目
函数y=log2(2x+1)的图象向右平移一个单位长度,横坐标伸长为原来的2倍,所得解析式为( )
| A、y=log2x |
| B、y=log2(2x-1) |
| C、y=log2(x+1) |
| D、y=log2(x-1) |
 已知抛物线x2=4y,过原点作斜率为1的直线交抛物线于第一象限内一点P1,又过点P1作斜率为
已知抛物线x2=4y,过原点作斜率为1的直线交抛物线于第一象限内一点P1,又过点P1作斜率为