题目内容
已知动点M(x,y)到两定点F1(0,2)、F2,(0,-2)距离之和为8.
(1)求点M(x,y)的轨迹C的方程;
(2)过点(0,3)作直线l与曲线C交于A,B两点,若OA⊥OB,求出直线l的方程.
(1)求点M(x,y)的轨迹C的方程;
(2)过点(0,3)作直线l与曲线C交于A,B两点,若OA⊥OB,求出直线l的方程.
考点:直线与圆锥曲线的综合问题
专题:圆锥曲线中的最值与范围问题
分析:(1)由于8>|F1F2|=4,可得点M(x,y)的轨迹C为椭圆,设标准方程为
+
=1(a>b>0).c=2,2a=8,利用b2=a2-c2即可得出.
(2)设直线l的方程为y=kx+3,A(x1,y1),B(x2,y2).与椭圆的方程联立可得(4+3k2)x2+18kx-21=0,得到根与系数的关系.由于OA⊥OB,可得
•
=x1x2+y1y2=(1+k2)x1x2+3k(x1+x2)+9=0.把根与系数的关系代入解出即可.
| y2 |
| a2 |
| x2 |
| b2 |
(2)设直线l的方程为y=kx+3,A(x1,y1),B(x2,y2).与椭圆的方程联立可得(4+3k2)x2+18kx-21=0,得到根与系数的关系.由于OA⊥OB,可得
| OA |
| OB |
解答:
解:(1)∵8>|F1F2|=4,
∴点M(x,y)的轨迹C为椭圆,
设标准方程为
+
=1(a>b>0).
则a=4,c=2,b2=a2-c2=12.
∴点M(x,y)的轨迹C的方程为:
+
=1.
(2)设直线l的方程为y=kx+3,A(x1,y1),B(x2,y2).
联立
,化为(4+3k2)x2+18kx-21=0,
△=(18k)2+84(4+3k2)>0,
∴x1+x2=
,x1x2=
.
∵OA⊥OB,
∴
•
=x1x2+y1y2=x1x2+(kx1+3)(kx2+3)=(1+k2)x1x2+3k(x1+x2)+9=0.
代入可得
-
+9=0,化为k2=
.
解得k=±
.
∴直线l的方程为:y=±
x+3.
∴点M(x,y)的轨迹C为椭圆,
设标准方程为
| y2 |
| a2 |
| x2 |
| b2 |
则a=4,c=2,b2=a2-c2=12.
∴点M(x,y)的轨迹C的方程为:
| y2 |
| 16 |
| x2 |
| 12 |
(2)设直线l的方程为y=kx+3,A(x1,y1),B(x2,y2).
联立
|
△=(18k)2+84(4+3k2)>0,
∴x1+x2=
| -18k |
| 4+3k2 |
| -21 |
| 4+3k2 |
∵OA⊥OB,
∴
| OA |
| OB |
代入可得
| -21(1+k2) |
| 4+3k2 |
| 54k2 |
| 4+3k2 |
| 5 |
| 16 |
解得k=±
| ||
| 4 |
∴直线l的方程为:y=±
| ||
| 4 |
点评:本题考查了直线与椭圆相交转化为方程联立可得根与系数的关系、向量垂直与数量积的关系,考查了推理能力与计算能力,属于难题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
已知集合A={a+2,(a+1)2,a2+3a+3},若1∈A,则实数a构成的集合B的元素个数是( )
| A、0 | B、1 | C、2 | D、3 |
函数y=log2(2x+1)的图象向右平移一个单位长度,横坐标伸长为原来的2倍,所得解析式为( )
| A、y=log2x |
| B、y=log2(2x-1) |
| C、y=log2(x+1) |
| D、y=log2(x-1) |
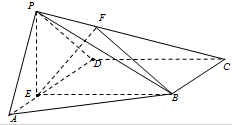 如图,在四棱锥P-ABCD中,E为AD上一点,PE⊥平面ABCD,AD∥BC,AD⊥CD,BC=ED=2AE=2,EB=3,F为PC上一点,且CF=2FP.
如图,在四棱锥P-ABCD中,E为AD上一点,PE⊥平面ABCD,AD∥BC,AD⊥CD,BC=ED=2AE=2,EB=3,F为PC上一点,且CF=2FP.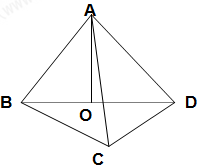 设A在平面BCD内的射影是直角三角形BCD的斜边BD的中点O,AC=BC=1,CD=
设A在平面BCD内的射影是直角三角形BCD的斜边BD的中点O,AC=BC=1,CD=