题目内容
6名学生排成一列，则学生甲、乙在学生丙不同侧的排位方法种数为 ．
考点：排列、组合的实际应用
专题：应用题,排列组合
分析：确定6名学生排成一列，共有
=720种，学生甲、乙在学生丙不同侧的概率为
，即可得出结论．
| A | 6 6 |
| 1 |
| 3 |
解答：
解：6名学生排成一列，共有
=720种，
甲、乙、丙的排列为
=6种，甲、乙在学生丙不同侧，有
=2种，
∴学生甲、乙在学生丙不同侧的概率为
，
∴学生甲、乙在学生丙不同侧的排位方法种数为720×
=240种，
故答案为：240．
| A | 6 6 |
甲、乙、丙的排列为
| A | 3 3 |
| A | 2 2 |
∴学生甲、乙在学生丙不同侧的概率为
| 1 |
| 3 |
∴学生甲、乙在学生丙不同侧的排位方法种数为720×
| 1 |
| 3 |
故答案为：240．
点评：本题考查排列、组合的实际应用，考查概率知识，考查学生的计算能力，比较基础．
练习册系列答案
全优冲刺100分系列答案
英才点津系列答案
相关题目
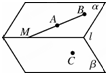如图，α∩β=l，A，B∈α，C∈β，且C∉l，直线AB∩l=M，过A，B，C三点的平面记作γ，则γ与β的交线必通过（ ）| A、点A | B、点B |
| C、点C但不过点M | D、点C和点M |
已知F1，F2是双曲线
-
=1（a＞0，b＞0）的焦点，以线段F1F2为边作正三角形MF1F2，若边MF1的中点在双曲线上，则双曲线的离心率是（ ）
| x2 |
| a2 |
| y2 |
| b2 |
A、4+2
| ||||
B、
| ||||
C、
| ||||
D、
|
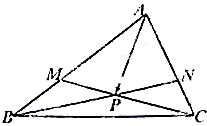在△ABC中，点M、N分别在边AB、AC上，且| AM |
| MB |
| AN |
| 3 |
| 5 |
| AC |
| AB |
| a |
| AC |
| b |
| AP |
| a |
| b |
A、
| ||||||||||
B、
| ||||||||||
C、
| ||||||||||
D、
|