题目内容
13.将函数f(x)=sin2x的图象向右平移$φ({0<φ<\frac{π}{2}})$个单位后得到函数g(x)的图象,若对满足|f(x1)-g(x2)|=2的x1,x2有$|{{x_1}-{x_2}}|=\frac{π}{6}$,则φ等于( )| A. | $\frac{5π}{12}$ | B. | $\frac{π}{3}$ | C. | $\frac{π}{4}$ | D. | $\frac{π}{6}$ |
分析 利用三角函数的最值,求出自变量x1,x2的值,然后判断选项即可.
解答 解:将函数f(x)=sin2x的图象向右平移$φ({0<φ<\frac{π}{2}})$个单位后得到函数g(x)=sin(2x-2φ)的图象,
若对满足|f(x1)-g(x2)|=2的x1,x2,有$|{{x_1}-{x_2}}|=\frac{π}{6}$,
故两个函数的最大值与最小值的差为2,有|x1-x2|min=$\frac{π}{6}$,
不妨设x1=$\frac{π}{4}$,x2=$\frac{5π}{12}$,则g(x2)=sin(2x2-2φ)=sin($\frac{5π}{6}$-2φ)=-1,
则φ的最小正值为$\frac{π}{6}$,检验满足条件,
故选:D.
点评 本题考查三角函数的图象平移,函数的最值以及函数的周期的应用,考查分析问题解决问题的能力,是好题,题目新颖.

练习册系列答案
相关题目
8.若当$\lim_{△x→0}\frac{{f({x_0})-f({x_0}+3△x)}}{2△x}$=1,则f′(x0)等于( )
| A. | $\frac{3}{2}$ | B. | $\frac{2}{3}$ | C. | -$\frac{3}{2}$ | D. | -$\frac{2}{3}$ |
18.阅读下面的程序框图,运行相应的程序,输出的结果为( )


| A. | -3 | B. | -$\frac{1}{2}$ | C. | $\frac{1}{3}$ | D. | 2 |
5.某算法的程序框图如图所示,若输出的y=$\frac{{\sqrt{2}}}{2}$,则输入的x的值可能为( )


| A. | $-\frac{1}{2}$ | B. | $\frac{1}{2}$ | C. | $\frac{3}{2}$ | D. | $\frac{9}{2}$ |
 中国古代有计算多项式值的秦九韶算法,如图是实现该算法的程序框图,执行该程序框图,若输入的x=2,n=2,依次输入的a为3,3,7,则输出的s=( )
中国古代有计算多项式值的秦九韶算法,如图是实现该算法的程序框图,执行该程序框图,若输入的x=2,n=2,依次输入的a为3,3,7,则输出的s=( )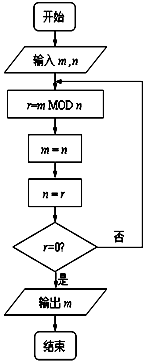 如图程序框图的算法思路源于数学名著《几何原本》中的“辗转相除法”,执行该程序框图(图中“mMOD n”表示m除以n的余数),若输入的m,n分别为72,15,则输出的m=( )
如图程序框图的算法思路源于数学名著《几何原本》中的“辗转相除法”,执行该程序框图(图中“mMOD n”表示m除以n的余数),若输入的m,n分别为72,15,则输出的m=( )