题目内容
沿矩形ABCD的对角线AC折起,形成空间四边形ABCD,使得二面角B-AC-D为120°,若AB=2,BC=1,则此时四面体ABCD的外接球的体积为 .
考点:球的体积和表面积
专题:计算题,空间位置关系与距离,球
分析:先确定球心的位置,然后求出球的半径,再解出外接球的体积.
解答:
解:由题意知,球心到四个顶点的距离相等,
则球心为对角线AC的中点,且其半径为AC长度的一半
=
,
则V球=
π×(
)3=
π.
故答案为:
π.
则球心为对角线AC的中点,且其半径为AC长度的一半
| 1 |
| 2 |
| 22+12 |
| ||
| 2 |
则V球=
| 4 |
| 3 |
| ||
| 2 |
5
| ||
| 6 |
故答案为:
5
| ||
| 6 |
点评:本题考查球的内接多面体,球的体积,外接球的半径与折叠二面角的大小没有关系,是解题的关键,考查学生发现问题解决问题的能力,是基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
如果f(x)为定义在R上的偶函数,且导数f′(x)存在,则f′(0)的值为( )
| A、2 | B、1 | C、0 | D、-1 |
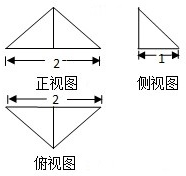 一个几何体的三视图及部分数据如图所示,正视图、侧视图和俯视图都是等腰直角三角形,则该几何体的外接球体积为
一个几何体的三视图及部分数据如图所示,正视图、侧视图和俯视图都是等腰直角三角形,则该几何体的外接球体积为