题目内容
已知向量
,
的夹角为45°,且|
|=1,|2
-
|=
,则|
|=( )
| a |
| b |
| a |
| a |
| b |
| 10 |
| b |
A、
| ||
B、2
| ||
C、3
| ||
D、4
|
考点:平面向量数量积的运算,向量的模
专题:平面向量及应用
分析:将|2
-
|=
平方,然后将夹角与|
|=1代入,得到|
|的方程,解方程可得.
| a |
| b |
| 10 |
| a |
| b |
解答:
解:因为向量
,
的夹角为45°,且|
|=1,|2
-
|=
,
所以4
2-4
•
+
2=10,即|
|2-2
|
|-6=0,
解得|
|=3
或|
|=-
(舍).
故选:C.
| a |
| b |
| a |
| a |
| b |
| 10 |
所以4
| a |
| a |
| b |
| b |
| b |
| 2 |
| b |
解得|
| b |
| 2 |
| b |
| 2 |
故选:C.
点评:本题解题的关键是将模转化为数量积,从而得到所求向量模的方程,利用到了方程的思想.

练习册系列答案
相关题目
已知锐角△ABC中,角A、B、C的对边长分别为a、b、c,向量
=(cosC+sinC,1),
=(cosC-sinC,
),且
⊥
.
(1)求角C的大小;
(2)若边c=2,求△ABC面积的最大值.
| m |
| n |
| 1 |
| 2 |
| m |
| n |
(1)求角C的大小;
(2)若边c=2,求△ABC面积的最大值.
已知集合A={(x,y)|y=log2x},B={(x,y)|y=2x},则A∩B=( )
| A、(0,+∞) | B、{1,2} |
| C、{(1,2)} | D、∅ |
 如图,M,N分别是空间四边形ABCD的棱AB,CD的中点,试判断向量
如图,M,N分别是空间四边形ABCD的棱AB,CD的中点,试判断向量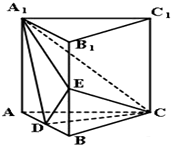 如图:直三棱柱ABC-A1B1C1中,AC=BC=AA1=2,∠ACB=90°.E为的中点,D点在AB上且DE=
如图:直三棱柱ABC-A1B1C1中,AC=BC=AA1=2,∠ACB=90°.E为的中点,D点在AB上且DE=