题目内容
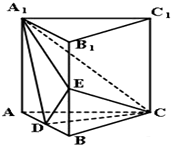 如图:直三棱柱ABC-A1B1C1中,AC=BC=AA1=2,∠ACB=90°.E为的中点,D点在AB上且DE=
如图:直三棱柱ABC-A1B1C1中,AC=BC=AA1=2,∠ACB=90°.E为的中点,D点在AB上且DE=| 3 |
(Ⅰ)求证:CD⊥平面A1ABB1;
(Ⅱ)求三棱锥A1-CDE中A1到平面CDE的距离.
考点:直线与平面垂直的判定
专题:空间位置关系与距离
分析:(1)先证明出CD⊥AB,进而根据直三棱柱的性质证明出CD⊥AA1,最后利用线面垂直的判定定理证明出 CD⊥平面A1ABB1
(2)根据S△A1DE=SA1ABB1-S△A1AD-S△DEB-S△A1B1E求得△A1DE的面积,进而求得三棱锥A1-CDE的体积为,然后求得△CDE面积,最后利用体积公式求得A1到平面CDE的距离.
(2)根据S△A1DE=SA1ABB1-S△A1AD-S△DEB-S△A1B1E求得△A1DE的面积,进而求得三棱锥A1-CDE的体积为,然后求得△CDE面积,最后利用体积公式求得A1到平面CDE的距离.
解答:
解:(1)在Rt△DBE中,BE=1,DE=
,
∴BD=
=
=
AB,
∴D为AB中点,而AC=BC,
∴CD⊥AB
又∵三棱柱ABC-A1B1C1为直三棱柱,
∴CD⊥AA1
又 AA1∩AB=A 且 AA1、AB?平面A1ABB1
∴CD⊥平面A1ABB1
(2)解:∵A1ABB1为矩形,
∴△A1AD,△DBE,△EB1A1都是直角三角形,
∴S△A1DE=SA1ABB1-S△A1AD-S△DEB-S△A1B1E
=2×2
-
×
×2-
×
×1-
×2
×1=
∴VA1-CDE=VC-A1DE=
×SA1DE×CD=
×
×
=1
∴三棱锥A1-CDE的体积为1.
S△CDE=
|CD||DE|=
×
×
=
故距离为
| 3 |
∴BD=
| DE2-BE2 |
| 2 |
| 1 |
| 2 |
∴D为AB中点,而AC=BC,
∴CD⊥AB
又∵三棱柱ABC-A1B1C1为直三棱柱,
∴CD⊥AA1
又 AA1∩AB=A 且 AA1、AB?平面A1ABB1
∴CD⊥平面A1ABB1
(2)解:∵A1ABB1为矩形,
∴△A1AD,△DBE,△EB1A1都是直角三角形,
∴S△A1DE=SA1ABB1-S△A1AD-S△DEB-S△A1B1E
=2×2
| 2 |
| 1 |
| 2 |
| 2 |
| 1 |
| 2 |
| 2 |
| 1 |
| 2 |
| 2 |
| 3 |
| 2 |
| 2 |
∴VA1-CDE=VC-A1DE=
| 1 |
| 3 |
| 1 |
| 3 |
| 3 |
| 2 |
| 2 |
| 2 |
∴三棱锥A1-CDE的体积为1.
S△CDE=
| 1 |
| 2 |
| 1 |
| 2 |
| 2 |
| 3 |
| ||
| 2 |
故距离为
| 6 |
点评:本题主要考查了线面垂直的判定定理,体积公式的运用,考查了学生空间观察能力和分析问题的能力.

练习册系列答案
相关题目
已知向量
,
的夹角为45°,且|
|=1,|2
-
|=
,则|
|=( )
| a |
| b |
| a |
| a |
| b |
| 10 |
| b |
A、
| ||
B、2
| ||
C、3
| ||
D、4
|
下列命题中,真命题是( )
A、sin(
| ||
| B、常数数列一定是等比数列 | ||
| C、一个命题的逆命题和否命题同真假 | ||
D、x+
|
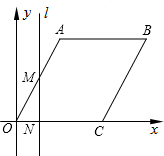 如图,在平面直角坐标系中,四边形OABC是菱形,点C的坐标为(4,0),∠AOC=60°,垂直于x轴的直线l从y轴出发,沿x轴正方向以每秒1个单位长度的速度向右平移,设直线l与菱形OABC的两边分别交于点M,N(点M在点N的上方),若△OMN的面积为S,直线l的运动时间为t秒(0≤t≤4),请求出S与t的函数关系.
如图,在平面直角坐标系中,四边形OABC是菱形,点C的坐标为(4,0),∠AOC=60°,垂直于x轴的直线l从y轴出发,沿x轴正方向以每秒1个单位长度的速度向右平移,设直线l与菱形OABC的两边分别交于点M,N(点M在点N的上方),若△OMN的面积为S,直线l的运动时间为t秒(0≤t≤4),请求出S与t的函数关系.