题目内容
10.已知曲线C的参数方程是$\left\{\begin{array}{l}{x=\frac{{t}^{2}}{4}}\\{y=t}\end{array}\right.$,直线l的方程是x=ky+1(k∈R).(Ⅰ)求曲线C的普通方程;
(Ⅱ)若直线l与曲线C相交所得的弦长是4,求实数k的值.
分析 (Ⅰ)消去t,可得曲线C的普通方程;
(Ⅱ)若直线l与曲线C相交所得的弦长是4,利用弦长公式建立方程,即可求实数k的值.
解答 解:(Ⅰ)曲线C的参数方程是$\left\{\begin{array}{l}{x=\frac{{t}^{2}}{4}}\\{y=t}\end{array}\right.$,消去t,可得曲线C的普通方程为y2=4x;
(Ⅱ)直线l与曲线C联立,得y2-4ky-4=0,
设交点坐标分别为(x1,y1),(x2,y2),则y1+y2=4k,y1y2=-4,
∵相交所得的弦长是4,∴$\sqrt{1+{k}^{2}}•\sqrt{16{k}^{2}+16}$,∴k=0.
点评 本题考查参数方程与普通方程的互化,考查弦长的计算,考查学生的计算能力,属于中档题.

练习册系列答案
 暑假作业暑假快乐练西安出版社系列答案
暑假作业暑假快乐练西安出版社系列答案
相关题目
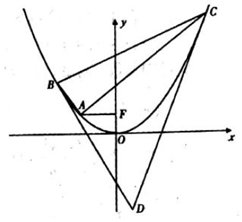 如图,点F是抛物线τ:x2=2py (p>0)的焦点,点A是抛物线上的定点,且$\overrightarrow{AF}$=(2,0),点B,C是抛物线上的动点,直线AB,AC斜率分别为k1,k2.
如图,点F是抛物线τ:x2=2py (p>0)的焦点,点A是抛物线上的定点,且$\overrightarrow{AF}$=(2,0),点B,C是抛物线上的动点,直线AB,AC斜率分别为k1,k2.