Question

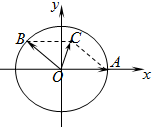如图，在xOy平面上，点A（1，0），点B在单位圆上，∠AOB=θ（0＜θ＜π），若

OA

+

OB

=

OC

，四边形OACB的面积用S_θ表示，则S_θ+

OA

•

OC

-1的取值范围为

 

．

Answer 1

考点：任意角的三角函数的定义

专题：三角函数的求值

分析：利用向量的数量积运算法则、平行四边形的面积计算公式可得S_θ+

OA

•

OC

-1=sinθ+cosθ，再利用两角和的正弦公式、正弦函数的值域，即可得出它的范围．

解答： 解：∵S_θ=|OA||OB|sinθ=sinθ，

OA

=（0，1），

OB

=（cosθ sinθ），
∴

OC

=

OA

+

OB

=（cosθ，1+sinθ），∴

OA

•

OC

=1+cosθ，
∴S_θ+

OA

•

OC

-1=sinθ+1+cosθ-1=cosθ+sinθ=

2

sin（θ+

π

4

）．
∵0＜θ＜π，∴

π

4

＜θ+

π

4

＜

5π

4

，∴-

2

2

＜sin（θ+

π

4

）≤1，∴-1＜

2

sin（θ+

π

4

）≤

2

，
故答案为：(-1，

2

]．

点评：本题综合考查了任意角的三角函数定义、半角公式、两角和差的正切公式、向量的数量积运算法则、平行四边形的面积计算公式、两角和的正弦公式等基础知识与基本技能方法，属于基础题．