题目内容
在△ABC中,角A,B,C所对的边分别为a,b,c,角A为锐角,且b=3asinB,则tan2A= .
考点:同角三角函数基本关系的运用
专题:解三角形
分析:先根据已知等式和正弦定理求得sinA的值,进而求得cosA和tanA的值,最后利用正切的两角和公式求得tan2A的值.
解答:
解:∵b=3asinB,
∴sinB=3sinAsinB,
∵sinB≠0,
∴sinA=
,
∵A为锐角,
∴cosA=
=
,
∴tanA=
=
,
∴tan2A=
=
=
,
故答案为:
.
∴sinB=3sinAsinB,
∵sinB≠0,
∴sinA=
| 1 |
| 3 |
∵A为锐角,
∴cosA=
| 1-sin2A |
2
| ||
| 3 |
∴tanA=
| 1 | ||
2
|
| ||
| 4 |
∴tan2A=
| 2tanA |
| 1-tan2A |
| ||||
1-
|
4
| ||
| 7 |
故答案为:
4
| ||
| 7 |
点评:本题主要考查了二倍角公式的应用,同角三角函数基本关系的应用.综合考查了学生对三角函数基础知识的综合运用.

练习册系列答案
 字词句篇与同步作文达标系列答案
字词句篇与同步作文达标系列答案 走进文言文系列答案
走进文言文系列答案
相关题目
在等差数列{an}中,若a2=2,a12=12,那么a4+a19=( )
| A、10 | B、23 | C、28 | D、60 |
已知定义在实数集R上的函数f(x)满足f(1)=3,且f(x)的导函数f′(x)<2,则不等式f(lnx)<2lnx+1的解集为( )
| A、(1,+∞) |
| B、(e,+∞) |
| C、(0,1) |
| D、(0,e) |
已知函数f(x)=
,若f(a)=0,则实数a的值等于( )
|
| A、-3 | B、1 |
| C、-3或1 | D、-1或3 |

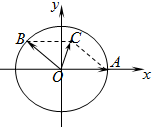 如图,在xOy平面上,点A(1,0),点B在单位圆上,∠AOB=θ(0<θ<π),若
如图,在xOy平面上,点A(1,0),点B在单位圆上,∠AOB=θ(0<θ<π),若