题目内容
将一根铁丝围成一个面积为4的矩形,则矩形周长的最小值为 .
考点:基本不等式
专题:不等式的解法及应用
分析:先根据题意表示出矩形的周长,进而根据基本不等式的性质求得周长的最小值.
解答:
解:设矩形的长为x,则宽为
,
则矩形周长为2x+
≥2
=8,2x=
,即x=2时,等号成立,
即矩形的周长的最小值为8,
故答案为:8.
| 4 |
| x |
则矩形周长为2x+
| 8 |
| x |
| 2×8 |
| 8 |
| x |
即矩形的周长的最小值为8,
故答案为:8.
点评:本题主要考查了基本不等式的应用.解题的过程注意满足的条件“一正,二定,三相等”.

练习册系列答案
相关题目
在等差数列{an}中,若a2=2,a12=12,那么a4+a19=( )
| A、10 | B、23 | C、28 | D、60 |
已知i为虚数单位,若复数z=1+i,则|z|的值为( )
A、
| ||
| B、2 | ||
C、
| ||
| D、3 |
任取一自然数,则该数平方的未位数是6的概率是( )
A、
| ||
B、
| ||
C、
| ||
D、
|
直线
(t为参数)被曲线x2-y2=1截得的弦长是( )
|
A、
| ||
B、2
| ||
C、
| ||
D、2
|
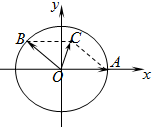 如图,在xOy平面上,点A(1,0),点B在单位圆上,∠AOB=θ(0<θ<π),若
如图,在xOy平面上,点A(1,0),点B在单位圆上,∠AOB=θ(0<θ<π),若