题目内容
求值：sin750°+cos（-660°）+tan（-135°）．
考点：运用诱导公式化简求值
专题：三角函数的求值
分析：利用诱导公式可得sin750°+cos（-660°）+tan（-135°）=sin30°+cos60°+tan45°，从而可得答案．
解答：
解：sin750°+cos（-660°）+tan（-135°）
=sin（2×360°+30°）+cos（-2×36°+60°）+tan（-180°+45°）
=sin30°+cos60°+tan45°
=
+
+1=2．
=sin（2×360°+30°）+cos（-2×36°+60°）+tan（-180°+45°）
=sin30°+cos60°+tan45°
=
| 1 |
| 2 |
| 1 |
| 2 |
点评：本题考查运用诱导公式化简求值，熟练掌握诱导公式是解决问题的关键，属于基础题．
练习册系列答案
相关题目
函数f（x）=x3+3x2+3x的单调增区间为（ ）
| A、（-∞，+∞） |
| B、（-∞，-1） |
| C、（0，+∞） |
| D、（-1，+∞） |
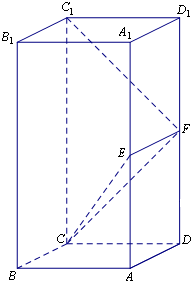在长方体ABCD-A1B1C1D1中，AA1=2AB，E，F分别是AA1，DD1的中点．