题目内容
已知O为原点，A，B是两定点，
=
，
=
，若2
=
，2
=
，则
= ．
| OA |
| a |
| OB |
| b |
| QA |
| AP |
| QB |
| BR |
| PR |
考点：平面向量的基本定理及其意义
专题：平面向量及应用
分析：2
=
，2
=
，可得2
-2
=
-
，2
-2
=
-
．两式相减即可得出．
| QA |
| AP |
| QB |
| BR |
| OA |
| OQ |
| OP |
| OA |
| OB |
| OQ |
| OR |
| OB |
解答：
解：∵2
=
，2
=
，
∴2
-2
=
-
，2
-2
=
-
．
则
=
-
=3
-3
=3
-3
．
故答案为：3
-3
．
| QA |
| AP |
| QB |
| BR |
∴2
| OA |
| OQ |
| OP |
| OA |
| OB |
| OQ |
| OR |
| OB |
则
| PR |
| OR |
| OP |
| OB |
| OA |
| b |
| a |
故答案为：3
| b |
| a |
点评：本题考查了向量的三角形法则、线性运算，考查了推理能力，属于基础题．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
“φ=2kπ+
，k∈Z”是“函数f（x）=cos（2x+φ）的图象过原点”的（ ）
| π |
| 2 |
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充分必要条件 |
| D、既不充分也不必要条件 |
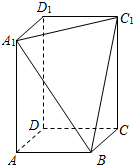在长方体ABCD-A1B1C1D1中，AB=BC=2，过A1、C1、B三点的平面截去长方体的一个角后，得到如图所示的几何体ABCD-A1C1D1，且这个几何体的体积为10．