题目内容
11.△ABC的顶点A(0,0),B(1,2),(3,-1),则该三角形面积为$\frac{7}{2}$.分析 法1:设出BC解析式,令y=0求出x的值,确定出D坐标,得到OD的长,三角形ABC面积=三角形ABD面积+三角形ACD面积,求出即可;
法2:利用两点间的距离公式求出三边长,再利用余弦定理求出cos∠BAC的值,利用同角三角函数间的基本关系求出sin∠BAC的值,根据三角形面积公式即可求出.
解答 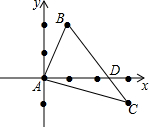 解:法1:设直线BC解析式为:y-2=$\frac{-1-2}{3-1}$(x-1),即3x+2y-7=0,
解:法1:设直线BC解析式为:y-2=$\frac{-1-2}{3-1}$(x-1),即3x+2y-7=0,
令y=0,得到x=$\frac{7}{3}$,即D($\frac{7}{3}$,0),
∴S△ABC=S△ABD+S△ACD=$\frac{1}{2}$×$\frac{7}{3}$×2+$\frac{1}{2}$×$\frac{7}{3}$×1=$\frac{7}{2}$;
法2:∵△ABC的顶点A(0,0),B(1,2),(3,-1),
∴AB=$\sqrt{5}$,AC=$\sqrt{10}$,BC=$\sqrt{(1-3)^{2}+(2+1)^{2}}$=$\sqrt{13}$,
∴cos∠BAC=$\frac{A{B}^{2}+A{C}^{2}-B{C}^{2}}{2AB•AC}$=$\frac{5+10-13}{10\sqrt{2}}$=$\frac{\sqrt{2}}{10}$,
∴sin∠BAC=$\frac{7\sqrt{2}}{10}$,
则S△ABC=$\frac{1}{2}$AB•ACsin∠BAC=$\frac{1}{2}$×$\sqrt{5}$×$\sqrt{10}$×$\frac{7\sqrt{2}}{10}$=$\frac{7}{2}$.
故答案为:$\frac{7}{2}$
点评 此题考查了正弦、余弦定理,以及两点间距离公式的应用,熟练掌握定理及公式是解本题的关键.

 寒假乐园北京教育出版社系列答案
寒假乐园北京教育出版社系列答案| A. | [-1,0] | B. | [1,2] | C. | [0,1] | D. | (-∞,1]∪[2,+∞) |
①命题“?x∈R,sinx≠1”的否定是“?x∈R,sinx=1”;
②数列{an}满足“an+1=3an”是“数列{an}为等比数列”的充分不必要条件;
③命题“若x=y,则sinx=siny”的逆否命题为真命题.
其中正确的是( )
| A. | ①②③ | B. | ①③ | C. | ①② | D. | ②③ |
| x | 4 | 5 | 6 | 7 |
| y | 8.2 | 7.8 | 6.6 | 5.4 |
| A. | -0.92 | B. | -0.94 | C. | -0.96 | D. | -0.98 |
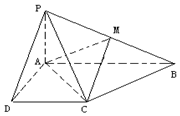 已知四棱锥P-ABCD的底面为直角梯形,AB∥DC,∠DAB=90°,PA⊥底面ABCD,且$PA=AD=DC=\frac{1}{2}$,AB=1,M是PB的中点
已知四棱锥P-ABCD的底面为直角梯形,AB∥DC,∠DAB=90°,PA⊥底面ABCD,且$PA=AD=DC=\frac{1}{2}$,AB=1,M是PB的中点 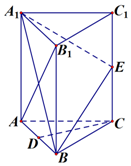 如图,在正三棱柱ABC-A1B1C1中,每条棱长均相等,D为棱AB的中点,E为侧棱CC1的中点.
如图,在正三棱柱ABC-A1B1C1中,每条棱长均相等,D为棱AB的中点,E为侧棱CC1的中点.