题目内容
设数列{an}的前n项和为Sn,且Sn=2an-p,其中p是不为零的常数.
(1)证明:数列{an}是等比数列
(2)当p=2时,若数列{bn}满足bn+1=bn+an(n∈N*),b1=2,求数列{bn}的前n项和Tn.
(1)证明:数列{an}是等比数列
(2)当p=2时,若数列{bn}满足bn+1=bn+an(n∈N*),b1=2,求数列{bn}的前n项和Tn.
考点:数列的求和
专题:等差数列与等比数列
分析:(1)由已知得an=2an-1,a1=p,由此能证明{an}是首项为p公比为2的等比数列.
(2)因为当p=2时,a1=2,则an=2n,由bn+1=bn+an(n∈N*),得bn+1-bn=2n,由累加法得bn=2n,由此能求出数列{bn}的前n项和.
(2)因为当p=2时,a1=2,则an=2n,由bn+1=bn+an(n∈N*),得bn+1-bn=2n,由累加法得bn=2n,由此能求出数列{bn}的前n项和.
解答:
(1)证明:因为Sn=2an-p,
则Sn-1=2an-1-p(n≥2),
所以当n≥2时,an=Sn-Sn-1=2an-2an-1,
整理得an=2an-1,
由Sn=2an-p,令n=1,得a1=2a1-p,
解得a1=p,
所以{an}是首项为p公比为2的等比数列.
(2)解:因为当p=2时,a1=2,则an=2n,
由bn+1=bn+an(n∈N*),得bn+1-bn=2n,
当n≥2时,由累加得
bn=b1+(b2-b1)+(b3-b2)+…+(bn-bn-1)
=2+2+22+…+2n-1
=2+
=2n,
∴数列{bn}的前n项和Tn=2+22+…+2n=
=2n+1-2.
则Sn-1=2an-1-p(n≥2),
所以当n≥2时,an=Sn-Sn-1=2an-2an-1,
整理得an=2an-1,
由Sn=2an-p,令n=1,得a1=2a1-p,
解得a1=p,
所以{an}是首项为p公比为2的等比数列.
(2)解:因为当p=2时,a1=2,则an=2n,
由bn+1=bn+an(n∈N*),得bn+1-bn=2n,
当n≥2时,由累加得
bn=b1+(b2-b1)+(b3-b2)+…+(bn-bn-1)
=2+2+22+…+2n-1
=2+
| 2(1-2n-1) |
| 1-2 |
=2n,
∴数列{bn}的前n项和Tn=2+22+…+2n=
| 2(1-2n) |
| 1-2 |
点评:本题考查等比数列的证明,考查数列的前n项和的求法,解题时要认真审题,注意累加法的合理运用.

练习册系列答案
相关题目
下列说法不正确的是( )
| A、命题“若x>0且y>0,则x+y>0”的否命题是假命题 | ||
| B、命题“?x0∈R,x02-x0-1<0”的否定是“?x∈R,x2-x-1≥0” | ||
C、“φ=
| ||
| D、a<0时,幂函数y=xa在(0,+∞)上单调递减 |
若平面α的法向量为
,直线l的方向向量为
,直线l与平面α的夹角为θ,则下列关系式成立的是( )
| n |
| a |
A、cos θ=
| ||
B、cos θ=
| ||
C、sin θ=
| ||
D、sin θ=
|
在平面直角坐标系xOy中,设不等式组
,表示的平面区域为D,在D内任取一整点P(横、纵坐标都是整数)测P落在区域
内的概率为( )
|
|
A、
| ||
B、
| ||
C、
| ||
D、
|
8cos410°-6cos20°+
sin40°=( )
| 3 |
A、
| ||||
| B、3 | ||||
C、
| ||||
D、
|
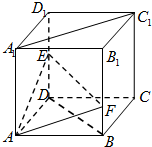 如图,在棱长为a的正方体ABCD-A1B1C1D1中,点E是棱D1D的中点,点F在棱B1B上,
如图,在棱长为a的正方体ABCD-A1B1C1D1中,点E是棱D1D的中点,点F在棱B1B上,