题目内容
已知定义域为R的函数f(x)=(
-1)是奇函数.
(1)求a的值;
(2)用单调性的定义证明f(x)在(-∞,+∞)上为减函数;
(3)若实数m满足f(1-2m)+f(
+1)≤0,求m的取值范围.
| 2 |
| 2x+a |
(1)求a的值;
(2)用单调性的定义证明f(x)在(-∞,+∞)上为减函数;
(3)若实数m满足f(1-2m)+f(
| 2m |
| 3 |
考点:奇偶性与单调性的综合
专题:
分析:本题(1)可以利用函数f(x)的奇偶性定义,得到参数a的值;(2)直接利用函数的单调性定义进行证明;(3)根据函数的奇偶性和单调性,从而将函数值问题转化为自变量大小的比较,再解不等式,得到本题的结论.
解答:
(1)解:∵定义域为R的函数f(x)=
-1是奇函数,
∴f(-x)=-f(x),x∈R.
∴
-1=-
+1,
∴
+
=1,
∴(a-1)22x+(a-1)22x+(a-1)=0,
∴(a-1)[22x+(a+1)2x+1]=0,
∴a=1.
(2)证明:在(-∞,+∞)上任取两个数x1,x2,且x1<x2,
f(x2)-f(x1)=(
-1)-(
-1)=
,
∵x1<x2,
∴2x1<2x2,
∴2x1-2x2<0,2x1+1>0,2x2+1>0,
∴f(x2)-f(x1)<0,
∴f(x2)<f(x1),
∴f(x)在(-∞,+∞)上为减函数.
(3)∵奇函数f(x)在(-∞,+∞)上为减函数,
∴f(1-2m)+f(
+1)≤0可转化为:
f(1-2m)≤-f(
+1),
∴f(1-2m)≤f(-
-1),
∴f(1-2m)≤f(-
-1),
∴1-2m≥-
-1,
∴m≤
.
∴m的取值范围是(-∞,
].
| 2 |
| 2x+a |
∴f(-x)=-f(x),x∈R.
∴
| 2 |
| 2x+a |
| 2 |
| 2-x+a |
∴
| 1 |
| 2x+a |
| 1 |
| 2-x+a |
∴(a-1)22x+(a-1)22x+(a-1)=0,
∴(a-1)[22x+(a+1)2x+1]=0,
∴a=1.
(2)证明:在(-∞,+∞)上任取两个数x1,x2,且x1<x2,
f(x2)-f(x1)=(
| 2 |
| 2x2+1 |
| 2 |
| 2x1+1 |
| 2(2x1-2x2) |
| (2x1+1)(2x2+1) |
∵x1<x2,
∴2x1<2x2,
∴2x1-2x2<0,2x1+1>0,2x2+1>0,
∴f(x2)-f(x1)<0,
∴f(x2)<f(x1),
∴f(x)在(-∞,+∞)上为减函数.
(3)∵奇函数f(x)在(-∞,+∞)上为减函数,
∴f(1-2m)+f(
| 2m |
| 3 |
f(1-2m)≤-f(
| 2m |
| 3 |
∴f(1-2m)≤f(-
| 2m |
| 3 |
∴f(1-2m)≤f(-
| 2m |
| 3 |
∴1-2m≥-
| 2m |
| 3 |
∴m≤
| 3 |
| 2 |
∴m的取值范围是(-∞,
| 3 |
| 2 |
点评:本题考查了函数的奇偶性、单调性及其应用,本题有一定的思维难度,属于中档题.

练习册系列答案
相关题目
已知集合A={y|y=log2x,x>1},B={y|y=(
)x,x>1},则(∁RA)∪B=( )
| 1 |
| 2 |
A、{y|y<
| ||
| B、{y|y≤0或y>1} | ||
C、{y|
| ||
| D、R |
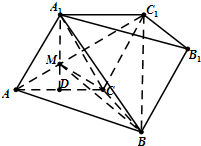 已知斜三棱柱ABC-A1B1C1中,四边形A1ACC1为菱形,∠ACB=90°,AC=BC=2,点D为AC的中点,A1D⊥平面ABC.
已知斜三棱柱ABC-A1B1C1中,四边形A1ACC1为菱形,∠ACB=90°,AC=BC=2,点D为AC的中点,A1D⊥平面ABC.