题目内容
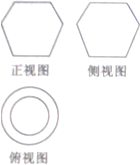
如图所示是某一容器的三视图,现向容器中匀速注水,容器中水面的高度h随时间t变化的可能图象是( )

A、 |
B、 |
C、 |
D、 |
考点:函数的图象
专题:函数的性质及应用
分析:根据几何体的三视图确定几何体的形状是解决本题的关键,可以判断出该几何体是上面和下面比较小,中间比较的粗的容器,判断出高度h随时间t变化的可能图象.
解答:
解:单位时间内水面上升的高度是递增的,最初递增的速度越来越慢,当快超过中间时,递增的速度越来越快,
故容器中水面的高度h随时间t变化是先快再慢后快,但是一致都在增加,
故选:D
故容器中水面的高度h随时间t变化是先快再慢后快,但是一致都在增加,
故选:D
点评:本题考查函数图象的辨别能力,考查学生对两变量变化趋势的直观把握能力,通过曲线的变化快慢进行筛选,体现了基本的数形结合思想.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
若一直线上有一点在已知平面外,则下列结论中正确的是( )
| A、直线与平面平行 |
| B、直线与平面相交 |
| C、直线上至少有一个点在平面内 |
| D、直线上有无数多个点都在平面外 |
已知数列{an}的前n项和是Sn,且Sn+
an=1(n∈N*).
(Ⅰ)求数列{an}的通项公式;
(Ⅱ)设bn=-3log3
+1(n∈N*),求
+
+…+
的值.
| 1 |
| 2 |
(Ⅰ)求数列{an}的通项公式;
(Ⅱ)设bn=-3log3
| an |
| 2 |
| 1 |
| b1b2 |
| 1 |
| b2b3 |
| 1 |
| b20b21 |
已知函数f(x)=
,若|f(x)|≥ax,则a的取值范围是( )
|
| A、(-∞,0] |
| B、(-∞,1] |
| C、[-2,1] |
| D、[-2,0] |
已知正三棱柱ABC-A1B1C1的底面边长为2,侧棱长为
,则三棱锥A1-B1BC的体积为( )
| 3 |
A、
| ||||
B、
| ||||
| C、1 | ||||
D、
|
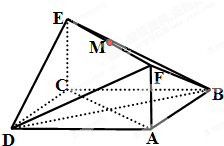 如图所示,已知正方形ABCD和矩形ACEF所在的平面互相垂直,AB=
如图所示,已知正方形ABCD和矩形ACEF所在的平面互相垂直,AB=