题目内容
17.为降低汽车尾气的排放量,某厂生产甲乙两种不同型号的节排器,分别从甲乙两种节排器中各自抽取100件进行性能质量评估检测,综合得分情况的频率分布直方图如图所示.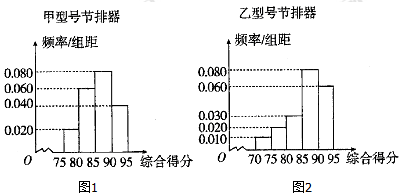
节排器等级及利润如表格表示,其中$\frac{1}{10}<a<\frac{1}{7}$
| 综合得分k的范围 | 节排器等级 | 节排器利润率 |
| k≥85 | 一级品 | a |
| 75≤k<85 | 二级品 | 5a2 |
| 70≤k<75 | 三级品 | a2 |
(2)视频率分布直方图中的频率为概率,用样本估计总体,则
①若从乙型号节排器中随机抽取3件,求二级品数ξ的分布列及数学期望E(ξ);
②从长期来看,骰子哪种型号的节排器平均利润较大?
分析 (1)利用互斥事件概率加法公式能求出至少有2件一级品的概率.
(2)①由已知及频率分布直方图中的信息知,乙型号节排器中的一级品的概率为$\frac{7}{10}$,二级品的概率$\frac{1}{4}$,三级品的概率为$\frac{1}{20}$,若从乙型号节排器随机抽取3件,则二级品数ξ所有可能的取值为0,1,2,3,且$ξ~B(3,\frac{1}{4})$,由此能求出ξ的分布列和数学期望.
②由题意分别求出甲型号节排器的利润的平均值和乙型号节排器的利润的平均值,由此求出投资乙型号节排器的平均利润率较大.
解答 解:(1)至少有2件一级品的概率$P=\frac{C_6^2C_4^1+C_6^3}{{C_{10}^3}}=\frac{2}{3}$.
(2)①由已知及频率分布直方图中的信息知,乙型号节排器中的一级品的概率为$\frac{7}{10}$,
二级品的概率$\frac{1}{4}$,三级品的概率为$\frac{1}{20}$,若从乙型号节排器随机抽取3件,
则二级品数ξ所有可能的取值为0,1,2,3,且$ξ~B(3,\frac{1}{4})$,
所以$P(ξ=0)=C_3^0{(\frac{3}{4})^3}{(\frac{1}{4})^0}=\frac{27}{64},P(ξ=1)=C_3^1{(\frac{3}{4})^2}{(\frac{1}{4})^1}=\frac{27}{64}$,
$P(ξ=2)=C_3^2{(\frac{3}{4})^1}{(\frac{1}{4})^2}=\frac{9}{64},P(ξ=3)=C_3^3{(\frac{3}{4})^0}{(\frac{1}{4})^3}=\frac{1}{64}$,
所以ξ的分布列为
| ξ | 0 | 1 | 2 | 3 |
| P | $\frac{27}{64}$ | $\frac{27}{64}$ | $\frac{9}{64}$ | $\frac{1}{64}$ |
②由题意知,甲型号节排器的利润的平均值${E_1}=\frac{3}{5}a+\frac{2}{5}×5{a^2}=2{a^2}+\frac{3}{5}a$,
乙型号节排器的利润的平均值${E_2}=\frac{7}{10}a+\frac{1}{4}×5{a^2}+\frac{1}{20}{a^2}=\frac{13}{10}{a^2}+\frac{7}{10}a$,
${E_1}-{E_2}=\frac{7}{10}{a^2}-\frac{1}{10}a=\frac{7}{10}a(a-\frac{1}{7})$,又$\frac{1}{10}<a<\frac{1}{7}$,
所以投资乙型号节排器的平均利润率较大.
点评 本题考查概率的求法,考查离散型随机变量的分布列和数学期望的求法及应用,是中档题,解题时要认真审题,注意排列组合知识的合理运用.

 小学生10分钟口算测试100分系列答案
小学生10分钟口算测试100分系列答案| A. | 充分非必要 | B. | 必要非充分 | ||
| C. | 充分必要 | D. | 既非充分又非必要 |
| A. | ?a>2,x1+x2=0 | B. | ?a>2,x1+x2=1 | C. | ?a>2,|x1-x2|=2 | D. | ?a>2,|x1-x2|=3 |
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
| A. | “若a>1,则a2>1”的否命题是“若a>1,则a2≤1” | |
| B. | {an}为等比数列,则“a1<a2<a3”是“a4<a5”的既不充分也不必要条件 | |
| C. | 若a,b∈R,则|a|+|b|>1是|a+b|>1的充分而不必要条件 | |
| D. | “$tanα≠\sqrt{3}$”必要不充分条件是“$α≠\frac{π}{3}$” |