题目内容
9.设函数f(x)的定义域为D,若存在非零实数l使得对于任意x∈M(M⊆D),有x+l∈D,且f(x+l)≥f(x),则称f(x)为M上的l高调函数.如果定义域是[-1,+∞)的函数f(x)=x2为[-1,+∞)上的m高调函数,那么实数m的取值范围是m≥2.分析 根据题意可知在[-1,+∞)上的任意x(设x=x+m)有y≥-1恒成立,推断出m≥-1-x恒成立,进而根据x的范围可推知-1-x最大为0,判断出m的范围,进而根据f(x+m)≥f(x),求得(x+m)2≥x2,化简求得m≥-2x恒成立,进而根据x的范围确定-2x的范围,进而求得m的范围.
解答 解:在[-1,+∞)上的任意x(设x=x+m)有y≥-1恒成立,则x+m≥-1恒成立,即m≥-1-x恒成立.
对于x∈[-1,+∞),当x=-1时-1-x最大为0,所以有m≥0.
又因为f(x+m)≥f(x),即(x+m)2≥x2在x∈[-1,+∝)上恒成立,化简得m2+2mx≥0,
又因为m≥0,所以m+2x≥0即m≥-2x恒成立,当x=-1时-2x最大为2,所以m≥2
综上可知m≥2.
故答案为m≥2.
点评 本题主要考查了抽象函数极其应用.考查了学生分析问题和解决问题的能力.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
19.已知a=2log20.3,b=20.1,c=0.21.3,则a,b,c的大小关系是( )
| A. | c>b>a | B. | c>a>b | C. | a>b>c | D. | b>c>a |
20.已知命题p:?x∈(2,+∞),x2<2x,命题q:?x0∈R,lnx0=x0-1,则下列命题中为真命题的是( )
| A. | p∧q | B. | ?p∧q | C. | p∧?q | D. | ¬p∧¬q |
17.为降低汽车尾气的排放量,某厂生产甲乙两种不同型号的节排器,分别从甲乙两种节排器中各自抽取100件进行性能质量评估检测,综合得分情况的频率分布直方图如图所示.
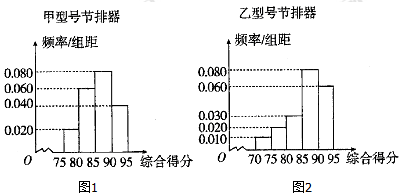
节排器等级及利润如表格表示,其中$\frac{1}{10}<a<\frac{1}{7}$
(1)若从这100件甲型号节排器按节排器等级分层抽样的方法抽取10件,再从这10件节排器中随机抽取3件,求至少有2件一级品的概率;
(2)视频率分布直方图中的频率为概率,用样本估计总体,则
①若从乙型号节排器中随机抽取3件,求二级品数ξ的分布列及数学期望E(ξ);
②从长期来看,骰子哪种型号的节排器平均利润较大?

节排器等级及利润如表格表示,其中$\frac{1}{10}<a<\frac{1}{7}$
| 综合得分k的范围 | 节排器等级 | 节排器利润率 |
| k≥85 | 一级品 | a |
| 75≤k<85 | 二级品 | 5a2 |
| 70≤k<75 | 三级品 | a2 |
(2)视频率分布直方图中的频率为概率,用样本估计总体,则
①若从乙型号节排器中随机抽取3件,求二级品数ξ的分布列及数学期望E(ξ);
②从长期来看,骰子哪种型号的节排器平均利润较大?
4.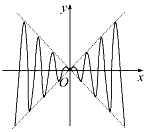 如图,虚线部分是平面直角坐标系四个象限的角平分线,实线部分是函数y=f(x)的部分图象,则f(x)可能是( )
如图,虚线部分是平面直角坐标系四个象限的角平分线,实线部分是函数y=f(x)的部分图象,则f(x)可能是( )
 如图,虚线部分是平面直角坐标系四个象限的角平分线,实线部分是函数y=f(x)的部分图象,则f(x)可能是( )
如图,虚线部分是平面直角坐标系四个象限的角平分线,实线部分是函数y=f(x)的部分图象,则f(x)可能是( )| A. | x2sinx | B. | xsinx | C. | x2cosx | D. | xcosx |
14.已知点M,N是抛物线y=4x2上不同的两点,F为抛物线的焦点,且满足$∠MFN=\frac{2π}{3}$,弦MN的中点P到直线l:$y=-\frac{1}{16}$的距离记为d,若|MN|2=λ•d2,则λ的最小值为( )
| A. | 3 | B. | $\sqrt{3}$ | C. | $1+\sqrt{3}$ | D. | 4 |
1.已知函数f(x)=$\frac{1}{3}$x3-$\frac{1}{2}$ax2+x在区间($\frac{1}{2}$,3)上既有极大值又有极小值,则实数a的取值范围是( )
| A. | (2,+∞) | B. | [2,+∞) | C. | (2,$\frac{5}{2}$) | D. | (2,$\frac{10}{3}$) |
18.若函数f(x)=$\frac{4x}{{x}^{2}+1}$在区间(m,2m+1)上是单调递增函数,则实数m的取值范围为( )
| A. | (-1,0] | B. | (-1,0) | C. | [0,1] | D. | (0,1] |
19.设函数f(x)在(m,n)上的导函数为g(x),x∈(m,n),若g(x)的导函数小于零恒成立,则称函数f(x)在(m,n)上为“凸函数”.已知当a≤2时,$f(x)=\frac{1}{6}{x^3}-\frac{1}{2}a{x^2}+x$,在x∈(-1,2)上为“凸函数”,则函数f(x)在(-1,2)上结论正确的是( )
| A. | 有极大值,没有极小值 | B. | 没有极大值,有极小值 | ||
| C. | 既有极大值,也有极小值 | D. | 既无极大值,也没有极小值 |