题目内容
12．已知x＞0，当$x+\frac{81}{x}$的值最小时x的值为9．分析 利用基本不等式的性质即可得出．
解答 解：x＞0，$x+\frac{81}{x}$≥$2\sqrt{x•\frac{81}{x}}$=18，当且仅当x=9时取等号．
故答案为：9．
点评 本题考查了不等式的性质，考查了推理能力与计算能力，属于基础题．
练习册系列答案
相关题目
20．已知命题p：?x∈（2，+∞），x2＜2x，命题q：?x0∈R，lnx0=x0-1，则下列命题中为真命题的是（ ）
| A． | p∧q | B． | ?p∧q | C． | p∧?q | D． | ￢p∧￢q |
17．为降低汽车尾气的排放量，某厂生产甲乙两种不同型号的节排器，分别从甲乙两种节排器中各自抽取100件进行性能质量评估检测，综合得分情况的频率分布直方图如图所示．
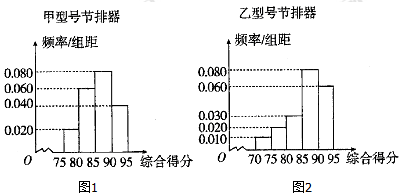
节排器等级及利润如表格表示，其中$\frac{1}{10}＜a＜\frac{1}{7}$
（1）若从这100件甲型号节排器按节排器等级分层抽样的方法抽取10件，再从这10件节排器中随机抽取3件，求至少有2件一级品的概率；
（2）视频率分布直方图中的频率为概率，用样本估计总体，则
①若从乙型号节排器中随机抽取3件，求二级品数ξ的分布列及数学期望E（ξ）；
②从长期来看，骰子哪种型号的节排器平均利润较大？
节排器等级及利润如表格表示，其中$\frac{1}{10}＜a＜\frac{1}{7}$
| 综合得分k的范围 | 节排器等级 | 节排器利润率 |
| k≥85 | 一级品 | a |
| 75≤k＜85 | 二级品 | 5a2 |
| 70≤k＜75 | 三级品 | a2 |
（2）视频率分布直方图中的频率为概率，用样本估计总体，则
①若从乙型号节排器中随机抽取3件，求二级品数ξ的分布列及数学期望E（ξ）；
②从长期来看，骰子哪种型号的节排器平均利润较大？
4．
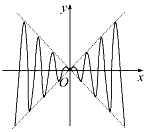如图，虚线部分是平面直角坐标系四个象限的角平分线，实线部分是函数y=f（x）的部分图象，则f（x）可能是（ ）
如图，虚线部分是平面直角坐标系四个象限的角平分线，实线部分是函数y=f（x）的部分图象，则f（x）可能是（ ）| A． | x2sinx | B． | xsinx | C． | x2cosx | D． | xcosx |
1．已知函数f（x）=$\frac{1}{3}$x3-$\frac{1}{2}$ax2+x在区间（$\frac{1}{2}$，3）上既有极大值又有极小值，则实数a的取值范围是（ ）
| A． | （2，+∞） | B． | [2，+∞） | C． | （2，$\frac{5}{2}$） | D． | （2，$\frac{10}{3}$） |