题目内容
3.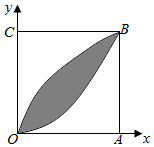 如图,在正方形OABC内.阴影部分是由两曲线y=$\sqrt{x}$,y=x2(0≤x≤1),在正方形内随机取一点,则此点取自阴影部分的概率是( )
如图,在正方形OABC内.阴影部分是由两曲线y=$\sqrt{x}$,y=x2(0≤x≤1),在正方形内随机取一点,则此点取自阴影部分的概率是( )| A. | $\frac{1}{6}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{2}$ | D. | $\frac{2}{3}$ |
分析 由定积分求阴影面积,由几何概型可得.
解答 解:由题意和定积分可得阴影部分面积:
S=${∫}_{0}^{1}$($\sqrt{x}$-x2)dx=($\frac{2}{3}$${x}^{\frac{3}{2}}$-$\frac{1}{3}$x3)${|}_{0}^{1}$=$\frac{2}{3}$-$\frac{1}{3}$=$\frac{1}{3}$,
∴由几何概型可得此点取自阴影部分的概率P=$\frac{1}{3}$
故选:B
点评 本题考查几何概型,涉及定积分求面积,属基础题.

练习册系列答案
 互动英语系列答案
互动英语系列答案
相关题目
13.椭圆$\left\{\begin{array}{l}{x=4+2cosθ}\\{y=1+5sinθ}\end{array}\right.$(θ为参数)的焦距是( )
| A. | $\sqrt{21}$ | B. | 2$\sqrt{21}$ | C. | $\sqrt{29}$ | D. | 2$\sqrt{29}$ |
11.某市近10年的国内生产总值从1000亿元开始以8%的速度增长,则这个城市近10年的国内生产总值一共是( )
| A. | 12500(1.089-1)亿元 | B. | 12500(1.0810-1)亿元 | ||
| C. | 12500(1-0.929)亿元 | D. | 12500(1-0.9210)亿元 |
18.过双曲线C:$\frac{{x}^{2}}{4}-\frac{{y}^{2}}{5}$=1的右焦点F作一直线(不平行于坐标轴)交双曲线于A、B两点,若点M是AB的中点,O为坐标原点,则kAB•kOM的值为( )
| A. | $\frac{5}{4}$ | B. | -$\frac{5}{4}$ | C. | $\frac{4}{5}$ | D. | -$\frac{4}{5}$ |