题目内容

13．椭圆$\left\{\begin{array}{l}{x=4+2cosθ}\\{y=1+5sinθ}\end{array}\right.$（θ为参数）的焦距是（　　）
A．$\sqrt{21}$B．2$\sqrt{21}$C．$\sqrt{29}$D．2$\sqrt{29}$

分析 把参数方程化成普通方程，根据椭圆的性质计算焦距．

解答 解：椭圆的普通方程为$\frac{（x-4）^{2}}{4}+\frac{（y-1）^{2}}{25}=1$，
∴椭圆的焦距为2$\sqrt{25-4}$=2$\sqrt{21}$．
故选：B．

点评 本题考查了椭圆的参数方程与普通方程的转化，属于基础题．

练习册系列答案
相关题目
3．对于定义在[0，+∞）上的函数f（x），若函数y=f（x）-（ax+b）满足：①在区间[0，+∞）上单调递减；②存在常数p，使其值域为（0，p]，则称函数g（x）=ax+b为f（x）的“渐近函数”；
（I）证明：函数 g（x）=x+1是函数f（x）=$\frac{{x}^{2}+2x+3}{x+1}$，x∈[0，+∞）的渐近函数，并求此时实数p的值；
（Ⅱ）若函数f（x）=$\sqrt{{x}^{2}+1}$，x∈[0，+∞），g（x）=ax，证明：当0＜a＜1时，g（x）不是f（x）的渐近函数．
4．2015年署期，某高校3名大学生计划去学校指定的A、B、C、D4个单位做暑假工，每人选择其中一个单位（可以去相同的单位），求选择A单位的人数的分布列．
1．已知A、B为椭圆$\frac{{x}^{2}}{4}$+$\frac{{y}^{2}}{3}$=1与双曲线$\frac{{x}^{2}}{4}$$-\frac{{y}^{2}}{3}$=1的公共顶点M、N分别为椭圆和双曲线上一点（异于点A、B），$\overrightarrow{AM}$$+\overrightarrow{BM}$=λ（$\overrightarrow{AN}$$+\overrightarrow{BN}$）（λ∈R），设直线AM、BM、AN、BN的斜率分别为k1、k2、k3、k4，则k1+k2+k3+k4=（　　）
A．-$\frac{3}{2}$B．0C．$\frac{3}{2}$D．$\frac{4\sqrt{3}}{3}$
8．已知数列{an}，a1=1且3an+1-3an=1，则a301等于101．
18．已知向量$\overrightarrow{a}$=（m，2），$\overrightarrow{b}$=（1，n-1），若$\overrightarrow{a}$⊥$\overrightarrow{b}$，则2m+4n的最小值为（　　）
A．2B．2$\sqrt{2}$C．4D．8
5．已知圆C过点M（1，1），N（5，1），且圆心在直线y=x-2上，则圆C的方程为（　　）
A．x2+y2-6x-2y+6=0B．x2+y2+6x-2y+6=0C．x2+y2+6x+2y+6=0D．x2+y2-2x-6y+6=0
2．已知复数z1=a+2i，z2=-2+i，且|z1|=|z2|，则实数a等于（　　）
A．1B．-1C．1或-1D．±1或0
3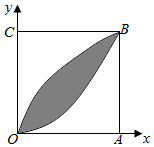．如图，在正方形OABC内．阴影部分是由两曲线y=$\sqrt{x}$，y=x2（0≤x≤1），在正方形内随机取一点，则此点取自阴影部分的概率是（　　）
A．$\frac{1}{6}$B．$\frac{1}{3}$C．$\frac{1}{2}$D．$\frac{2}{3}$

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网