题目内容
8．在一批产品中共12件，其中次品3件，每次从中任取一件，在取得合格品之前取出的次品数ξ的所有可能取值是0，1，2，3．分析 由已知条件能求出在取得合格品之前取出的次品数ξ的所有可能取值．
解答 解：∵在一批产品中共12件，其中次品3件，每次从中任取一件，
∴在取得合格品之前取出的次品数ξ的所有可能取值是0，1，2，3．
故答案为：0，1，2，3．
点评 本题考查离散型随机变量的可能取值的求法，是基础题，解题时要认真审题，注意离散型随机变量的性质的合理运用．
练习册系列答案
相关题目
18．已知向量$\overrightarrow{a}$=（m，2），$\overrightarrow{b}$=（1，n-1），若$\overrightarrow{a}$⊥$\overrightarrow{b}$，则2m+4n的最小值为（ ）
| A． | 2 | B． | 2$\sqrt{2}$ | C． | 4 | D． | 8 |
3．
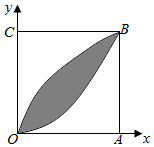如图，在正方形OABC内．阴影部分是由两曲线y=$\sqrt{x}$，y=x2（0≤x≤1），在正方形内随机取一点，则此点取自阴影部分的概率是（ ）
如图，在正方形OABC内．阴影部分是由两曲线y=$\sqrt{x}$，y=x2（0≤x≤1），在正方形内随机取一点，则此点取自阴影部分的概率是（ ）| A． | $\frac{1}{6}$ | B． | $\frac{1}{3}$ | C． | $\frac{1}{2}$ | D． | $\frac{2}{3}$ |
13．随机变量X的分布列如下，则m=（ ）
| X | 1 | 2 | 3 | 4 |
| P | $\frac{1}{4}$ | m | $\frac{1}{3}$ | $\frac{1}{6}$ |
| A． | $\frac{1}{3}$ | B． | $\frac{1}{2}$ | C． | $\frac{1}{6}$ | D． | $\frac{1}{4}$ |
8．双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1（a＞0，b＞0）的一条渐近线方程是y=$\frac{4}{3}$x，则该双曲线的离心率是（ ）
| A． | $\frac{5}{4}$ | B． | $\frac{5}{3}$ | C． | $\frac{7}{3}$ | D． | $\frac{\sqrt{21}}{3}$ |
9．设双曲线$\frac{{x}^{2}}{2}$-$\frac{{y}^{2}}{{b}^{2}}$=1（b＞0）与抛物线y2=8x交于两点A，B，且|AB|=8，则该双曲线的焦点到其渐近线的距离为（ ）
| A． | $\frac{1}{3}$ | B． | $\frac{2}{3}$ | C． | 4 | D． | $\frac{\sqrt{6}}{3}$ |