题目内容
18．过双曲线C：$\frac{{x}^{2}}{4}-\frac{{y}^{2}}{5}$=1的右焦点F作一直线（不平行于坐标轴）交双曲线于A、B两点，若点M是AB的中点，O为坐标原点，则kAB•kOM的值为（ ）| A． | $\frac{5}{4}$ | B． | -$\frac{5}{4}$ | C． | $\frac{4}{5}$ | D． | -$\frac{4}{5}$ |
分析 设M（a，b），A（x1，y1），B（x2，y2），易知kOM=$\frac{b}{a}$，再由点差法可知kAB=$\frac{{y}_{1}-{y}_{2}}{{x}_{1}-{x}_{2}}$=$\frac{5a}{4b}$，由此可求出kAB•kOM=$\frac{5}{4}$．
解答 解：设M（a，b），A（x1，y1），B（x2，y2），
∵M为AB的中点，∴x1+x2=2a，y1+y2=2b，
把A、B代入双曲线C：$\frac{{x}^{2}}{4}-\frac{{y}^{2}}{5}$=1，得
$\frac{1}{4}$x12-$\frac{1}{5}$y12=1，$\frac{1}{4}$x22-$\frac{1}{5}$y22=1，
两式相减得$\frac{1}{4}$（x1+x2）（x1-x2）=$\frac{1}{5}$（y1+y2）（y1-y2），
∴$\frac{1}{2}$a（x1-x2）=$\frac{2}{5}$b（y1-y2），
∴kAB=$\frac{{y}_{1}-{y}_{2}}{{x}_{1}-{x}_{2}}$=$\frac{5a}{4b}$，
∵kOM=$\frac{b}{a}$，∴kAB•kOM=$\frac{5}{4}$．
故选：A．
点评 本题考查双曲线的性质和应用，解题时要注意点差法的合理运用，同时考查中点坐标公式和直线的斜率公式的运用，属于中档题．
练习册系列答案
中考利剑中考试卷汇编系列答案
教育世家状元卷系列答案
黄冈课堂作业本系列答案
单元加期末复习先锋大考卷系列答案
相关题目
9．已知点A是抛物线C：x2=2py（p＞0）上一点，O为坐标原点，若A，B是以点M（0，10）为圆心，|OA|的长为半径的圆与抛物线C的两个公共点，且△ABO为等边三角形，则p的值是（ ）
| A． | $\frac{5}{2}$ | B． | $\frac{5}{3}$ | C． | $\frac{5}{6}$ | D． | $\frac{5}{9}$ |
6．已知抛物线C：y2=2px（p＞0）的焦点为F，点A，B在C上，且点F是△AOB的重心，则cos∠AFB为（ ）
| A． | -$\frac{3}{5}$ | B． | -$\frac{7}{8}$ | C． | -$\frac{11}{12}$ | D． | -$\frac{23}{25}$ |
3．
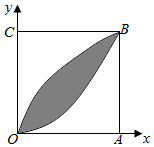如图，在正方形OABC内．阴影部分是由两曲线y=$\sqrt{x}$，y=x2（0≤x≤1），在正方形内随机取一点，则此点取自阴影部分的概率是（ ）
如图，在正方形OABC内．阴影部分是由两曲线y=$\sqrt{x}$，y=x2（0≤x≤1），在正方形内随机取一点，则此点取自阴影部分的概率是（ ）| A． | $\frac{1}{6}$ | B． | $\frac{1}{3}$ | C． | $\frac{1}{2}$ | D． | $\frac{2}{3}$ |