题目内容
14.已知△ABC中,AB=8,BC=10,AC=6,P点在平面ABC内,且$\overrightarrow{PB}$•$\overrightarrow{PC}$=-9,则|$\overrightarrow{PA}$|的取值范围为[1,4+$\sqrt{7}$].分析 由已知得到三角形为直角三角形,构建坐标系,求出点P的轨迹方程,由此可以判断|$\overrightarrow{PA}$|的取值范围.
解答  解:∵AB=8,BC=10,AC=6,
解:∵AB=8,BC=10,AC=6,
∴AB2+BC2=BC2,
∴AB⊥AC,
以A为原点,以AB为x轴,以AC为y轴,建立坐标系,
则A(0,0),B(8,0),C(0,6),
设P(x,y),(0<x<8,0<y<6),
∴$\overrightarrow{PB}$=(8-x,-y),$\overrightarrow{PC}$=(-x,6-y),
∴$\overrightarrow{PB}$•$\overrightarrow{PC}$=-8x+x2-6y+y2=-9,即(x-4)2+(y-3)2=16,
∵|$\overrightarrow{PA}$|=$\sqrt{{x}^{2}+{y}^{2}}$,
∴当P点在AD的连线上时,|$\overrightarrow{PA}$|的取值最小,
∴|$\overrightarrow{PA}$|=|$\overrightarrow{AD}$|-|$\overrightarrow{PD}$|=$\sqrt{{4}^{2}+{3}^{2}}$-4=5-4=1,
当P点在x轴上时,|$\overrightarrow{PA}$|的取值最大,
即(x-4)2+(0-3)2=16,
解得x=4+$\sqrt{7}$或x=4-$\sqrt{7}$舍去,
故|$\overrightarrow{PA}$|的取值范围为[1,4+$\sqrt{7}$]
故答案为:[1,4+$\sqrt{7}$].
点评 本题考查平面向量的数量积的定义和性质,圆的有关知识,考查运算能力,属于中档题.

练习册系列答案
相关题目
5.已知圆C过点M(1,1),N(5,1),且圆心在直线y=x-2上,则圆C的方程为( )
| A. | x2+y2-6x-2y+6=0 | B. | x2+y2+6x-2y+6=0 | C. | x2+y2+6x+2y+6=0 | D. | x2+y2-2x-6y+6=0 |
2.已知复数z1=a+2i,z2=-2+i,且|z1|=|z2|,则实数a等于( )
| A. | 1 | B. | -1 | C. | 1或-1 | D. | ±1或0 |
9.已知点A是抛物线C:x2=2py(p>0)上一点,O为坐标原点,若A,B是以点M(0,10)为圆心,|OA|的长为半径的圆与抛物线C的两个公共点,且△ABO为等边三角形,则p的值是( )
| A. | $\frac{5}{2}$ | B. | $\frac{5}{3}$ | C. | $\frac{5}{6}$ | D. | $\frac{5}{9}$ |
6.已知抛物线C:y2=2px(p>0)的焦点为F,点A,B在C上,且点F是△AOB的重心,则cos∠AFB为( )
| A. | -$\frac{3}{5}$ | B. | -$\frac{7}{8}$ | C. | -$\frac{11}{12}$ | D. | -$\frac{23}{25}$ |
3.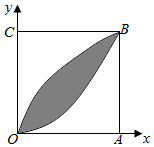 如图,在正方形OABC内.阴影部分是由两曲线y=$\sqrt{x}$,y=x2(0≤x≤1),在正方形内随机取一点,则此点取自阴影部分的概率是( )
如图,在正方形OABC内.阴影部分是由两曲线y=$\sqrt{x}$,y=x2(0≤x≤1),在正方形内随机取一点,则此点取自阴影部分的概率是( )
 如图,在正方形OABC内.阴影部分是由两曲线y=$\sqrt{x}$,y=x2(0≤x≤1),在正方形内随机取一点,则此点取自阴影部分的概率是( )
如图,在正方形OABC内.阴影部分是由两曲线y=$\sqrt{x}$,y=x2(0≤x≤1),在正方形内随机取一点,则此点取自阴影部分的概率是( )| A. | $\frac{1}{6}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{2}$ | D. | $\frac{2}{3}$ |