题目内容
3.已知双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1$的渐近线是y=±$\frac{4}{3}$x,则该双曲线的离心率$\frac{5}{3}$.分析 求出双曲线的渐近线方程,可得b=$\frac{4}{3}$a,由a,b,c的关系和离心率公式,计算即可得到所求值.
解答 解:双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1$的渐近线方程为y=±$\frac{b}{a}$x,
由题意可得$\frac{b}{a}$=$\frac{4}{3}$,即有b=$\frac{4}{3}$a,
c=$\sqrt{{a}^{2}+{b}^{2}}$=$\frac{5}{3}$a,
可得e=$\frac{c}{a}$=$\frac{5}{3}$,
故答案为:$\frac{5}{3}$.
点评 本题考查双曲线的离心率的求法,注意运用渐近线方程,考查运算能力,属于基础题.

练习册系列答案
 本土教辅赢在暑假高效假期总复习云南科技出版社系列答案
本土教辅赢在暑假高效假期总复习云南科技出版社系列答案 暑假作业北京艺术与科学电子出版社系列答案
暑假作业北京艺术与科学电子出版社系列答案 第三学期赢在暑假系列答案
第三学期赢在暑假系列答案
相关题目
2.已知复数z1=a+2i,z2=-2+i,且|z1|=|z2|,则实数a等于( )
| A. | 1 | B. | -1 | C. | 1或-1 | D. | ±1或0 |
3.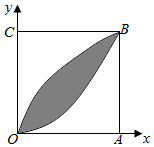 如图,在正方形OABC内.阴影部分是由两曲线y=$\sqrt{x}$,y=x2(0≤x≤1),在正方形内随机取一点,则此点取自阴影部分的概率是( )
如图,在正方形OABC内.阴影部分是由两曲线y=$\sqrt{x}$,y=x2(0≤x≤1),在正方形内随机取一点,则此点取自阴影部分的概率是( )
 如图,在正方形OABC内.阴影部分是由两曲线y=$\sqrt{x}$,y=x2(0≤x≤1),在正方形内随机取一点,则此点取自阴影部分的概率是( )
如图,在正方形OABC内.阴影部分是由两曲线y=$\sqrt{x}$,y=x2(0≤x≤1),在正方形内随机取一点,则此点取自阴影部分的概率是( )| A. | $\frac{1}{6}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{2}$ | D. | $\frac{2}{3}$ |
8.双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的一条渐近线方程是y=$\frac{4}{3}$x,则该双曲线的离心率是( )
| A. | $\frac{5}{4}$ | B. | $\frac{5}{3}$ | C. | $\frac{7}{3}$ | D. | $\frac{\sqrt{21}}{3}$ |
12.双曲线x2-$\frac{{y}^{2}}{4}$=1的渐近线方程为( )
| A. | y=±4x | B. | y=±2x | C. | y=±$\frac{1}{2}x$ | D. | y=±$\frac{1}{4}$x |
13.下列说法中正确的是( )
| A. | “f(0)=0”是“函数f(x)是奇函数”的充要条件 | |
| B. | “若$α=\frac{π}{6}$,则$sinα=\frac{1}{2}$”的否命题是“若$α≠\frac{π}{6}$,则$sinα≠\frac{1}{2}$ | |
| C. | 若$p:?{x_0}∈R,x_0^2-{x_0}-1>0$,则¬p:?x∈R,x2-x-1<0 | |
| D. | 若p∧q为假命题,则p,q均为假命题 |