题目内容
过圆内一点的最长弦与最短弦所在直线方程分别为(a+1)x+(2a-1)y+a+8=0与ax-2y+4=0,则实数a= .
考点:直线与圆相交的性质
专题:直线与圆
分析:根据过圆内一点的最长弦与最短弦所在直线互相垂直,可得
•
=-1,由此求得实数a的值.
| a+1 |
| 1-2a |
| a |
| 2 |
解答:
解:由于过圆内一点的最长弦与最短弦所在直线互相垂直,可得
•
=-1,
即(a-1)(a-2)=0,求得a=1,或a=2,
故答案为:1或2.
| a+1 |
| 1-2a |
| a |
| 2 |
即(a-1)(a-2)=0,求得a=1,或a=2,
故答案为:1或2.
点评:本题主要考查直线和圆相交的性质,两条直线垂直的性质,属于基础题.

练习册系列答案
相关题目
已知f(
)=
,则f′(x)等于( )
| 1 |
| x |
| x |
| 1+x |
A、
| ||
B、-
| ||
C、
| ||
D、-
|
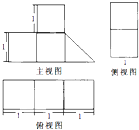
某几何体的三视图如图所示,则该几何体的体积为( )

A、
| ||
B、
| ||
C、
| ||
D、
|