题目内容
15.定义在(0,$\frac{π}{2}$)的函数f(x)=8sinx-tanx的最大值为$3\sqrt{3}$.分析 利用导函数研究其单调性,求其最大值.
解答 解:函数f(x)=8sinx-tanx,
那么:f′(x)=8cosx-$\frac{1}{co{s}^{2}x}$=$\frac{8co{s}^{3}x-1}{co{s}^{2}x}$,
令f′(x)=0,
得:cosx=$\frac{1}{2}$
∵x∈(0,$\frac{π}{2}$),
∴x=$\frac{π}{3}$.
当x∈(0,$\frac{π}{3}$)时,f′(x)>0,函数f(x)在区间(0,$\frac{π}{3}$)上是单调增函数.
当x∈($\frac{π}{3}$,$\frac{π}{2}$)时,f′(x)<0,函数f(x)在区间($\frac{π}{3}$,$\frac{π}{2}$)上是单调减函数.
∴当x=$\frac{π}{3}$时,函数f(x)取得最大值为$3\sqrt{3}$
故答案为:$3\sqrt{3}$.
点评 本题考查了利用导函数研究其单调性,求其最大值的问题.属于基础题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
6.指数函数y=ax(a>0,a≠1)的反函数图象过点(9,2),则a=( )
| A. | 3 | B. | 2 | C. | 9 | D. | 4 |
20.在等差数列{an}中,a3+a4+a5+a6+a7=400,则a2+a8=( )
| A. | 40 | B. | 80 | C. | 160 | D. | 320 |
7.已知F1、F2分别为椭圆$\frac{{x}^{2}}{2}$+y2=1的左右两个焦点,过F1作倾斜角为$\frac{π}{4}$的弦AB,则△F2AB的面积为( )
| A. | $\frac{2\sqrt{3}}{3}$ | B. | $\frac{4}{3}$ | C. | $\frac{4\sqrt{3}}{3}$ | D. | $\frac{4\sqrt{2}}{3}$-1 |
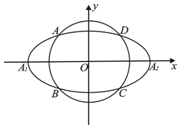 如图,椭圆C0:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0,a,b为常数),动圆C1:x2+y2=t12,b<t1<a..点A1,A2分别为C0的左,右顶点,C1与C0相交于A,B,C,D四点.
如图,椭圆C0:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0,a,b为常数),动圆C1:x2+y2=t12,b<t1<a..点A1,A2分别为C0的左,右顶点,C1与C0相交于A,B,C,D四点.