题目内容
13. 已知如图正四面体SABC的侧面积为$48\sqrt{3}$,O为底面正三角形ABC的中心.
已知如图正四面体SABC的侧面积为$48\sqrt{3}$,O为底面正三角形ABC的中心.(1)求证:SA⊥BC;
(2)求点O到侧面SABC的距离.
分析 (1)取BC的中点D,由等腰三角形的性质可得AD⊥BC,SD⊥BC,结合线面垂直的判定可得BC⊥平面SAD,进一步得到SA⊥BC;
(2)由(1)可知BC⊥平面SAD,过点O作OE⊥SD,得到OE⊥平面SBC,即OE就是点O到侧面SBC的距离.由题意可知点O在AD上,设正四面体SABC的棱长为a,利用等积法求得a,在等边三角形ABC中,D是BC的中点,求解直角三角形可得点O到侧面SBC的距离.
解答  (1)证明:取BC的中点D,连结AD,SD,
(1)证明:取BC的中点D,连结AD,SD,
∵△ABC是等边三角形,D是BC的中点,
∴AD⊥BC,
∵△SBC是等边三角形,D是BC的中点,
∴SD⊥BC,
∵AD∩SD=D,AD,SD?平面SAD,
∴BC⊥平面SAD,
∵SA?平面SAD,
∴SA⊥BC;
(2)解:由(1)可知BC⊥平面SAD,
∵BC?平面SBC,
∴平面SAD⊥平面SBC,
∵平面SAD∩平面SBC=SD,过点O作OE⊥SD,则OE⊥平面SBC,
∴OE就是点O到侧面SBC的距离.
由题意可知点O在AD上,设正四面体SABC的棱长为a,
∴${S}_{△SBC}=\frac{1}{2}SB•SC•sin60°=\frac{\sqrt{3}}{4}{a}^{2}$,
∵正四面体SABC的侧面积为$48\sqrt{3}$,
∴$3{S_{△SBC}}=3×\frac{{\sqrt{3}}}{4}{a^2}=48\sqrt{3}$,得a=8.
在等边三角形ABC中,D是BC的中点,
∴$AD=AC•sinC=\frac{{\sqrt{3}}}{2}a$.
同理可得$SD=\frac{{\sqrt{3}}}{2}a$.
∵O为底面正三角形ABC的中心,
∴$AO=\frac{2}{3}AD=\frac{{\sqrt{3}}}{3}a$,$OD=\frac{1}{3}AD=\frac{{\sqrt{3}}}{6}a$,
∴在Rt△SAO中,$SO=\sqrt{S{A^2}-A{O^2}}=\frac{{\sqrt{6}}}{3}a$,
由$\frac{1}{2}OD•SO=\frac{1}{2}SD•OE$,
得:$\frac{1}{2}×\frac{{\sqrt{3}}}{6}a×\frac{{\sqrt{6}}}{3}a=\frac{1}{2}×\frac{{\sqrt{3}}}{2}a•OE$,
∴$OE=\frac{{\sqrt{6}}}{9}a=\frac{{8\sqrt{6}}}{9}$,即点O到侧面SBC的距离为$\frac{{8\sqrt{6}}}{9}$.
点评 本题考查空间中直线与直线的位置关系,考查了空间想象能力和思维能力,训练了利用等积法求多面体的体积,是中档题.

 优学名师名题系列答案
优学名师名题系列答案| A. | (3,0) | B. | (3,3) | C. | (4,3) | D. | (6,3) |
| A. | 5π | B. | 20π | C. | 8π | D. | 16π |
| A. | 10 | B. | 9 | C. | 6 | D. | 5 |
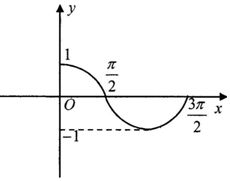 已知函数f(x)=sin(ωx+φ),x∈R(其中ω>0,-π<φ<π)的部分图象,如图所示.那么f(x)的解析式为( )
已知函数f(x)=sin(ωx+φ),x∈R(其中ω>0,-π<φ<π)的部分图象,如图所示.那么f(x)的解析式为( )| A. | $f(x)=sin(x+\frac{π}{2})$ | B. | $f(x)=sin(x-\frac{π}{2})$ | C. | $f(x)=sin(2x+\frac{π}{2})$ | D. | $f(x)=sin(2x-\frac{π}{2})$ |
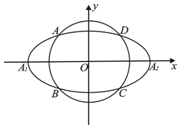 如图,椭圆C0:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0,a,b为常数),动圆C1:x2+y2=t12,b<t1<a..点A1,A2分别为C0的左,右顶点,C1与C0相交于A,B,C,D四点.
如图,椭圆C0:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0,a,b为常数),动圆C1:x2+y2=t12,b<t1<a..点A1,A2分别为C0的左,右顶点,C1与C0相交于A,B,C,D四点.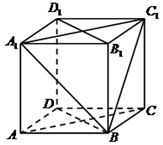 在正方体ABCD-A1B1C1D1中:
在正方体ABCD-A1B1C1D1中: