题目内容
已知圆C:(x-1)2+(y-2)2=
,直线l:(2m+1)x+(m+1)y-7m-4=0(m∈R).
(1)试讨论直线l与圆C的位置关系,并叙述理由;
(2)求直线被圆C截得的弦长最小时l的方程.
| 25 |
| 4 |
(1)试讨论直线l与圆C的位置关系,并叙述理由;
(2)求直线被圆C截得的弦长最小时l的方程.
考点:直线和圆的方程的应用
专题:直线与圆
分析:(1)首先求出直线恒过的定点P(3,1),然后利用点与点的距离与半径比较来判定直线l与圆C的位置关系:相交
(2)直线被圆C截得的弦长最小时l的方程:过P(3,1)垂直于经过圆心的直线.然后利用直线垂直的充要条件求得直线的斜率,进一步利用点斜式求得直线方程.
(2)直线被圆C截得的弦长最小时l的方程:过P(3,1)垂直于经过圆心的直线.然后利用直线垂直的充要条件求得直线的斜率,进一步利用点斜式求得直线方程.
解答:
解:(1)圆C:(x-1)2+(y-2)2=
则:圆心C(1,2)R=
直线l:(2m+1)x+(m+1)y-7m-4=0(m∈R).
2mx+x+my+y-7m-4=0(m∈R)
解得:
即直线l恒过定点P(3,1)
则:CP=
=
<
(2)由(1)得直线L恒过定点P(3,1),直线被圆C截得的弦长最小的直线是:过P(3,1)垂直于经过圆心的直线.
则k1=
=-
由于:直线与直线的垂直
∴k1•k2=-1
解得:k2=2
∴直线被圆C截得的弦长最小时l的方程:y-1=2(x-3)
即:2x-y-5=0
故答案为:(1)相交
(2)2x-y-5=0
| 25 |
| 4 |
则:圆心C(1,2)R=
| 5 |
| 2 |
直线l:(2m+1)x+(m+1)y-7m-4=0(m∈R).
2mx+x+my+y-7m-4=0(m∈R)
|
|
即直线l恒过定点P(3,1)
则:CP=
| (3-1)2+(1-2)2 |
| 5 |
| 5 |
| 2 |
(2)由(1)得直线L恒过定点P(3,1),直线被圆C截得的弦长最小的直线是:过P(3,1)垂直于经过圆心的直线.
则k1=
| 2-1 |
| 1-3 |
| 1 |
| 2 |
由于:直线与直线的垂直
∴k1•k2=-1
解得:k2=2
∴直线被圆C截得的弦长最小时l的方程:y-1=2(x-3)
即:2x-y-5=0
故答案为:(1)相交
(2)2x-y-5=0
点评:本题考查的知识点:圆的标准方程,恒过定点的直线方程,利用点与圆的位置关系判断直线与圆的位置关系,直线垂直的充要条件,恒过圆内一定点且被圆所截的最短弦的直线方程,直线点斜式的应用及相关的运算问题.

练习册系列答案
相关题目
如果一个钝角三角形的边长是三个连续自然数,那么最长边的长度为( )
| A、3 | B、4 | C、6 | D、7 |
已知复数z=i-
,(其中i是虚数单位),则
=( )
| 1 |
| i |
. |
| z |
| A、0 | ||
B、
| ||
| C、-2i | ||
| D、2i |
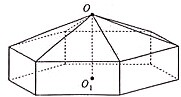 请您设计一个帐篷,它下部的形状是高为1m的正六棱柱,上部的形状是侧棱长为3m的正六棱锥(如图所示).试问当帐篷的顶点O到底面中心O1的距离为多少时,帐篷的体积为16
请您设计一个帐篷,它下部的形状是高为1m的正六棱柱,上部的形状是侧棱长为3m的正六棱锥(如图所示).试问当帐篷的顶点O到底面中心O1的距离为多少时,帐篷的体积为16