题目内容
某市居民自来水收费标准如下:每户每月用水量不超过25吨时,按每吨3.2元收费;当每户每月用水量超过25吨时,其中25吨按每吨为3.2元收费,超过25吨的部分按每吨4.80元收费.设每户每月用水量为x吨,应交水费y元.
(1)求y关于x的函数关系;
(2)某用户1月份用水量为30吨,则1月份应交水费多少元?
(3)若甲、乙两用户1月用水量之比为5:3,共交水费228.8元,分别求出甲、乙两用户该月的用水量和水费.
(1)求y关于x的函数关系;
(2)某用户1月份用水量为30吨,则1月份应交水费多少元?
(3)若甲、乙两用户1月用水量之比为5:3,共交水费228.8元,分别求出甲、乙两用户该月的用水量和水费.
考点:分段函数的应用
专题:应用题,函数的性质及应用
分析:(1)根据某市居民自来水收费标准,分段求出各段上每户每月用水量为x吨与应交水费y元之间的函数关系式,最后综合讨论结果可得答案.
(2)将x=30代入(1)中所得函数的解析式,可得1月份应交水费
(3)设甲、乙两用户1月用水量分别为5m吨,3m吨,根据(1)中所得函数的解析式,分别讨论m,结合甲、乙两用户共交水费228.8元,解方程可得答案.
(2)将x=30代入(1)中所得函数的解析式,可得1月份应交水费
(3)设甲、乙两用户1月用水量分别为5m吨,3m吨,根据(1)中所得函数的解析式,分别讨论m,结合甲、乙两用户共交水费228.8元,解方程可得答案.
解答:
解:(1)由题意得:
当0<x≤25时,y=3.2x
当x>25时,y=25×3.2+4.8×(x-25)=80+4.8(x-25)
∴y=
(2)当x=30时,y=80+4.8×(30-25)=104,
故1月份应交水费104元
(3)若甲、乙两用户1月用水量分别为5m,3m,
①若m≤5,则甲、乙两用户共交水费8m×3.2≤128元,不合题意;
②若5<m≤
,则甲、乙两用户共交水费80+4.8(5m-25)+3.2×3m=33.6m-40=228.8元,m=8;
甲用户用水量为40吨,交费152元,乙用户用水量为24吨,交费76.8元.
③若m>
,则甲、乙两用户共交水费80+4.8(5m-25)+80+4.8(3m-25)=38.4m-80≥240元,不合题意;
答:甲用户用水量为40吨,交费152元,乙用户用水量为24吨,交费76.8元. 16分.
当0<x≤25时,y=3.2x
当x>25时,y=25×3.2+4.8×(x-25)=80+4.8(x-25)
∴y=
|
(2)当x=30时,y=80+4.8×(30-25)=104,
故1月份应交水费104元
(3)若甲、乙两用户1月用水量分别为5m,3m,
①若m≤5,则甲、乙两用户共交水费8m×3.2≤128元,不合题意;
②若5<m≤
| 25 |
| 3 |
甲用户用水量为40吨,交费152元,乙用户用水量为24吨,交费76.8元.
③若m>
| 25 |
| 3 |
答:甲用户用水量为40吨,交费152元,乙用户用水量为24吨,交费76.8元. 16分.
点评:本题是分段函数的简单应用题,关键是列出函数解析式,找对自变量的分段区间.

练习册系列答案
 精英口算卡系列答案
精英口算卡系列答案 应用题点拨系列答案
应用题点拨系列答案 状元及第系列答案
状元及第系列答案
相关题目
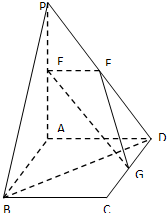 如图,平面PAD⊥平面ABCD,ABCD为正方形,∠PAD=90°,且PA=AD=2,E,F,G分别是线段PA、PD、CD的中点.
如图,平面PAD⊥平面ABCD,ABCD为正方形,∠PAD=90°,且PA=AD=2,E,F,G分别是线段PA、PD、CD的中点.