题目内容
已知函数f(x)=ax2+xlnx,(a∈R)
(1)当a=0时,求f(x)的最小值;
(2)在区间(1,2)内任取两个实数p,q(p≠q),若不等式
>1恒成立,求实数a的取值范围;
(3)求证:
+
+
+…+
<
(其中n>1,n∈N*,e=2.71828…).
(1)当a=0时,求f(x)的最小值;
(2)在区间(1,2)内任取两个实数p,q(p≠q),若不等式
| f(p+1)-f(q+1) |
| p-q |
(3)求证:
| ln2 |
| 23 |
| ln3 |
| 33 |
| ln |
| 43 |
| lnn |
| n3 |
| 1 |
| e |
考点:函数恒成立问题,利用导数求闭区间上函数的最值
专题:函数的性质及应用,导数的综合应用,不等式的解法及应用
分析:(1)把a=0代入函数解析式,然后直接利用导数求最小值;
(2)把
化为
,表示点(p+1,f(p+1))与点(q+1,f(q+1))连线的斜率,即函数图象在区间(2,3)任意两点连线的斜率大于1,即f′(x)=2ax+lnx+1>1在x∈(2,3)内恒成立.然后利用分离变量法结合导数得答案;
(3)由(2)得,-
≥g(e),即得到
≤
,然后利用错位相减法求数列的和,放缩后得答案.
(2)把
| f(p+1)-f(q+1) |
| p-q |
| f(p+1)-f(q+1) |
| (p+1)-(q+1) |
(3)由(2)得,-
| lnx |
| x |
| lnx |
| x3 |
| 1 |
| e |
| 1 |
| x2 |
解答:
(1)解:∵a=0时,f(x)=xlnx(x>0),
由f′(x)=1+lnx>0,得x>
,
∴f(x)在(0,
)上递减,在(
,+∞)上递增.
∴f(x)min=f(
)=-
;
(2)解:
=
,
表示点(p+1,f(p+1))与点(q+1,f(q+1))连线的斜率,又1<p<2,1<q<2,
∴2<p+1<3,2<q+1<3,即函数图象在区间(2,3)任意两点连线的斜率大于1,
即f′(x)=2ax+lnx+1>1在x∈(2,3)内恒成立.
∴当x∈(2,3)时,2a≥-
恒成立.
∴2a≥(-
)max.
设g(x)=-
,x∈(2,3),
则g′(x)=
.
若g′(x)=0,则x=e.
当2<x<e时,g′(x)<0,g(x)在(2,e)上单调递减;当e<x<3时,g′(x)>0,g(x)在(e,3)上单调递增.
又g(2)=-
>g(3)=-
,
∴2a≥-
.
故a≥-
;
(3)由(2)得,-
≥g(e),
∴
≤
,
∴
≤
,
∴
+
+…+
≤
(
+
+…+
),
又
+
+…+
<
+
+…+
=(1-
)+(
-
)+…+(
-
)=1-
<1,
∴
+
+
+…+
<
.
由f′(x)=1+lnx>0,得x>
| 1 |
| e |
∴f(x)在(0,
| 1 |
| e |
| 1 |
| e |
∴f(x)min=f(
| 1 |
| e |
| 1 |
| e |
(2)解:
| f(p+1)-f(q+1) |
| p-q |
| f(p+1)-f(q+1) |
| (p+1)-(q+1) |
表示点(p+1,f(p+1))与点(q+1,f(q+1))连线的斜率,又1<p<2,1<q<2,
∴2<p+1<3,2<q+1<3,即函数图象在区间(2,3)任意两点连线的斜率大于1,
即f′(x)=2ax+lnx+1>1在x∈(2,3)内恒成立.
∴当x∈(2,3)时,2a≥-
| lnx |
| x |
∴2a≥(-
| lnx |
| x |
设g(x)=-
| lnx |
| x |
则g′(x)=
| lnx-1 |
| x2 |
若g′(x)=0,则x=e.
当2<x<e时,g′(x)<0,g(x)在(2,e)上单调递减;当e<x<3时,g′(x)>0,g(x)在(e,3)上单调递增.
又g(2)=-
| ln2 |
| 2 |
| ln3 |
| 3 |
∴2a≥-
| ln2 |
| 2 |
故a≥-
| ln2 |
| 4 |
(3)由(2)得,-
| lnx |
| x |
∴
| lnx |
| x |
| 1 |
| e |
∴
| lnx |
| x3 |
| 1 |
| e |
| 1 |
| x2 |
∴
| ln2 |
| 23 |
| ln3 |
| 33 |
| lnn |
| n3 |
| 1 |
| e |
| 1 |
| 22 |
| 1 |
| 32 |
| 1 |
| n2 |
又
| 1 |
| 22 |
| 1 |
| 32 |
| 1 |
| n2 |
| 1 |
| 1×2 |
| 1 |
| 2×3 |
| 1 |
| (n-1)n |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| n |
| 1 |
| n+1 |
| 1 |
| n |
∴
| ln2 |
| 23 |
| ln3 |
| 33 |
| ln |
| 43 |
| lnn |
| n3 |
| 1 |
| e |
点评:本题考查了函数恒成立问题,考查了利用导数求函数的最值,训练了裂项相消法求数列的和,是压轴题.

练习册系列答案
相关题目
一个几何体的三视图如图所示,则该几何体的体积是( )


A、
| ||||
B、
| ||||
C、
| ||||
D、4
|
已知m,n是两条不同的直线,α,β是两个不同的平面,则下列命题正确的是( )
| A、若m∥α,n∥α,则m∥n |
| B、若m∥n,m⊥α,n?β,则α⊥β |
| C、若m∥α,m∥β,则α∥β |
| D、若m∥α,α⊥β,则m⊥β |
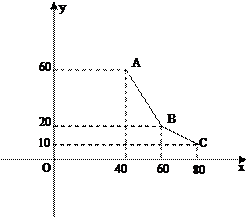 小张经营某一消费品专卖店,已知该消费品的进价为每件40元,该店每月销售量y(百件)与销售单价x(元/件)之间的关系用如图的一折线表示,职工每人每月工资为1000元,该店还应交付的其它费用为每月10000元.
小张经营某一消费品专卖店,已知该消费品的进价为每件40元,该店每月销售量y(百件)与销售单价x(元/件)之间的关系用如图的一折线表示,职工每人每月工资为1000元,该店还应交付的其它费用为每月10000元. 已知函数f(x)是定义在R上的偶函数,已知x≥0时,f(x)=x2-2x.
已知函数f(x)是定义在R上的偶函数,已知x≥0时,f(x)=x2-2x.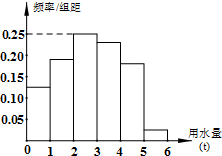 某市为了解全市居民日常用水量的分布情况,现采用抽样调查的方式,获得了n位居民某年的月均用水量(单位:t),样本统计结果如图表:
某市为了解全市居民日常用水量的分布情况,现采用抽样调查的方式,获得了n位居民某年的月均用水量(单位:t),样本统计结果如图表: