题目内容
已知m，n是两条不同的直线，α，β是两个不同的平面，则下列命题正确的是（ ）
| A、若m∥α，n∥α，则m∥n |
| B、若m∥n，m⊥α，n?β，则α⊥β |
| C、若m∥α，m∥β，则α∥β |
| D、若m∥α，α⊥β，则m⊥β |
考点：空间中直线与直线之间的位置关系
专题：操作型,空间位置关系与距离
分析：对四个命题分别进行判断，即可得出结论．
解答：
解：若m∥α，n∥α，则m∥n或m，n相交、异面，即A不正确；
∵直线m⊥平面α，直线n?平面β，m∥n，∴α⊥β．故B成立；
若m∥α，m∥β，则α∥β或m与α、β交线平行，即C不正确；
若m∥α，α⊥β，则m可以与β垂直、平行，相交或m?β，即D不正确．
故选：B．
∵直线m⊥平面α，直线n?平面β，m∥n，∴α⊥β．故B成立；
若m∥α，m∥β，则α∥β或m与α、β交线平行，即C不正确；
若m∥α，α⊥β，则m可以与β垂直、平行，相交或m?β，即D不正确．
故选：B．
点评：本题考查直线与平面的位置关系的合理运用，考查学生分析解决问题的能力，比较基础．．
练习册系列答案
名校课堂系列答案
相关题目
已知函数f（x）=
，则f（f（
））=（ ）
|
| π |
| 4 |
| A、1 | B、-2 | C、2 | D、-1 |
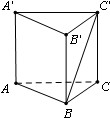如图，在三棱柱ABC-A′B′C′中，底面ABC是正三角形，AA′⊥底面ABC，且AB=1，AA′=2，则直线BC′与平面ABB′A′所成角的正弦值为已知f（x-1）=x2，则f（x）的解析式为（ ）
| A、f（x）=x2-2x-1 |
| B、f（x）=x2-2x+1 |
| C、f（x）=x2+2x-1 |
| D、f（x）=x2+2x+1 |