题目内容
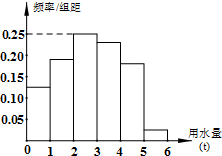 某市为了解全市居民日常用水量的分布情况,现采用抽样调查的方式,获得了n位居民某年的月均用水量(单位:t),样本统计结果如图表:
某市为了解全市居民日常用水量的分布情况,现采用抽样调查的方式,获得了n位居民某年的月均用水量(单位:t),样本统计结果如图表:(Ⅰ)分别求出x,n,y的值;
(Ⅱ)若从样本中月均用水量在[5,6]内的5位居民a,b,c,d,e中任选2人作进一步的调查研究,求居民a被选中的概率.
| 分组 | 频数 | 频率 |
| [0,1) | 25 | y |
| [1,2) | 0.19 | |
| [2,3) | 50 | x |
| [3,4) | 0.23 | |
| [4,5) | 0.18 | |
| [5,6] | 5 |
考点:频率分布直方图
专题:概率与统计
分析:(Ⅰ)由频率分布直方图得出月均用水量在[2,3)的频率,从而求出x、n、y的值;
(Ⅱ)用列举法写出“居民a被选中”的基本事件以及从5位居民中任选2人的基本事件数,求出概率即可.
(Ⅱ)用列举法写出“居民a被选中”的基本事件以及从5位居民中任选2人的基本事件数,求出概率即可.
解答:
解:(Ⅰ)由频率分布直方图得,
月均用水量在[2,3)的频率为0.25,即x=0.25;
又∵
=x=0.25,∴n=200;…(4分)
∴y=
=0.125;…(6分)
(Ⅱ)记“居民a被选中”为事件A,∴基本事件为:
(a,b),(a,c),(a,d),(a,e),
(b,c),(b,d),(b,e),
(c,d),(c,e),(d,e);
共计10个基本事件;…(10分)
事件A包含的基本事件有
(a,b),(a,c),(a,d),(a,e),共4个,…(11分)
∴居民a被选中的概率为P(A)=
=
.…(12分)
月均用水量在[2,3)的频率为0.25,即x=0.25;
又∵
| 50 |
| n |
∴y=
| 25 |
| 200 |
(Ⅱ)记“居民a被选中”为事件A,∴基本事件为:
(a,b),(a,c),(a,d),(a,e),
(b,c),(b,d),(b,e),
(c,d),(c,e),(d,e);
共计10个基本事件;…(10分)
事件A包含的基本事件有
(a,b),(a,c),(a,d),(a,e),共4个,…(11分)
∴居民a被选中的概率为P(A)=
| 4 |
| 10 |
| 2 |
| 5 |
点评:本题考查了频率分布直方图的应用问题,也考查了古典概型的概率问题,是基础题.

练习册系列答案
 期末宝典单元检测分类复习卷系列答案
期末宝典单元检测分类复习卷系列答案
相关题目
已知f(x-1)=x2,则f(x)的解析式为( )
| A、f(x)=x2-2x-1 |
| B、f(x)=x2-2x+1 |
| C、f(x)=x2+2x-1 |
| D、f(x)=x2+2x+1 |
下列函数中,在区间(0,+∞)上递减的偶函数是( )
| A、y=x3+1 | ||
| B、y=log2(|x|+2) | ||
C、y=(
| ||
| D、y=2|x| |