题目内容
已知不等式kx2-x+4k<0(k≠0).
(1)若不等式的解集为{x|x<-4或x>-1},求实数k的值;
(2)若不等式的解集为∅,求实数k的取值范围.
(1)若不等式的解集为{x|x<-4或x>-1},求实数k的值;
(2)若不等式的解集为∅,求实数k的取值范围.
考点:一元二次不等式的解法
专题:不等式的解法及应用
分析:(1)由题设条件,根据二次函数与方程的关系,得:k<0,且-4,-1是方程kx2-x+4k=0的两个实数根,再由韦达定理能求出k的值,(2)题意可知k>0且△≤0.列不等式组求解即可.
解答:
解:(1)∵不等式kx2-x+4k<0(k≠0)的解集为{x|x<-4或x>-1},
-4,-1是方程kx2-x+4k=0的两个实数根,则-4-1=
,解得k=-
,
(2)∵不等式kx2-x+4k<0(k≠0)的解集为∅,
∴
,解得k≥
,
所以实数k的取值范围是[
,+∞).
-4,-1是方程kx2-x+4k=0的两个实数根,则-4-1=
| 1 |
| k |
| 1 |
| 5 |
(2)∵不等式kx2-x+4k<0(k≠0)的解集为∅,
∴
|
| 1 |
| 4 |
所以实数k的取值范围是[
| 1 |
| 4 |
点评:本题考查一元二次不等式的解法及其应用,是基础题.解题时要认真审题,仔细解答.

练习册系列答案
 名校名师培优作业本加核心试卷系列答案
名校名师培优作业本加核心试卷系列答案 全程金卷系列答案
全程金卷系列答案
相关题目
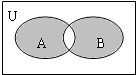 设全集U={x|x<9,且x∈Z},A={1,2,3},B={3,4,5,6},图中阴影部分所表示的集合为( )
设全集U={x|x<9,且x∈Z},A={1,2,3},B={3,4,5,6},图中阴影部分所表示的集合为( )| A、{1,2,3,4,5,6,7,8} |
| B、{1,2,4,5,6} |
| C、{1,2,4,5,6,7,8} |
| D、{1,2,3,4,5,6} |
在等比数列{an}中,已知a3+a6=9,a2a7=8,则a32+a62=( )
| A、9 | B、65 | C、72 | D、99 |
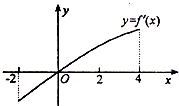 定义在[-2,+∞)的函数f(x)的部分值如下表,f(x)的导函数f(x)的图象如图,两正数a,b满足f(2a+b)<1,则
定义在[-2,+∞)的函数f(x)的部分值如下表,f(x)的导函数f(x)的图象如图,两正数a,b满足f(2a+b)<1,则| b+3 |
| a+3 |
A、(
| ||||
B、(
| ||||
C、(
| ||||
D、(-
|