题目内容
函数f(x)=psinωx(p>0,ω>0)的最大值为2,其图象相邻两条对称轴之间的距离为
.
(1)求函数f(x)的解析式;
(2)在△ABC中,AC=f(
),C=
,求△ABC周长的最大值.
| π |
| 2 |
(1)求函数f(x)的解析式;
(2)在△ABC中,AC=f(
| B |
| 2 |
| 2π |
| 3 |
考点:函数y=Asin(ωx+φ)的图象变换,由y=Asin(ωx+φ)的部分图象确定其解析式
专题:三角函数的求值,解三角形
分析:(1)利用最值可求p,利用图象相邻两条对称轴之间的距离为
确定ω;
(2)由(1)可得三角形b=2sinB,由此利用正弦定理可求外接圆的直径,并且将三角形的周长转化为角的解析式,利用三角函数两脚和与差的三角函数
公式化简三角函数为一个角的三角函数形式,求最值.
| π |
| 2 |
(2)由(1)可得三角形b=2sinB,由此利用正弦定理可求外接圆的直径,并且将三角形的周长转化为角的解析式,利用三角函数两脚和与差的三角函数
公式化简三角函数为一个角的三角函数形式,求最值.
解答:
解:(1)因为函数f(x)=psinωx(p>0,ω>0)的最大值为2,其图象相邻两条对称轴之间的距离为
.
所以p=2,T=π,∴ω=2,
∴f(x)=2sin2x;
(2)在△ABC中,AC=f(
),C=
,由(1)得AC=2sinB=b,由正弦定理可知,△ABC的外接圆直径为
=2,
△ABC周长为AB+BC+AC=a+b+c=2sinA+2sinB+2sinC=2sinA+2sin(
-A)+
=sinA+
cosA+
=2sin(A+
)+
,其中
<A+
<
,
所以A+
=
时△ABC周长的最大值为2+
.
| π |
| 2 |
所以p=2,T=π,∴ω=2,
∴f(x)=2sin2x;
(2)在△ABC中,AC=f(
| B |
| 2 |
| 2π |
| 3 |
| b |
| sinB |
△ABC周长为AB+BC+AC=a+b+c=2sinA+2sinB+2sinC=2sinA+2sin(
| π |
| 3 |
| 3 |
| 3 |
| 3 |
| π |
| 3 |
| 3 |
| π |
| 3 |
| π |
| 3 |
| 2π |
| 3 |
所以A+
| π |
| 3 |
| π |
| 2 |
| 3 |
点评:本题考查由y=Asin(ωx+φ)的解析式确定、三角函数的恒等变换及化简求值,考查计算能力.

练习册系列答案
相关题目
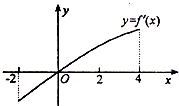 定义在[-2,+∞)的函数f(x)的部分值如下表,f(x)的导函数f(x)的图象如图,两正数a,b满足f(2a+b)<1,则
定义在[-2,+∞)的函数f(x)的部分值如下表,f(x)的导函数f(x)的图象如图,两正数a,b满足f(2a+b)<1,则| b+3 |
| a+3 |
A、(
| ||||
B、(
| ||||
C、(
| ||||
D、(-
|
在正方体ABCD-A1B1C1D1中与AD1成600角的面对角线的条数是( )
| A、4条 | B、6条 | C、8条 | D、10条 |
为研究某大学女大学生的身高xcm和体重ykg的相关关系,据所抽取8名女生测得的数据可计算出线性回归方程为
=0.849x-85.712,由此方程知,当x=172(cm)时,y=60.316(kg),下列说法正确的是( )
 |
| y |
| A、身高为172cm的女大学生的体重是60.316kg |
| B、身高为172cm的所有女大学生的平均体重必为60.316kg |
| C、身高为172cm的女大学生的体重多数在60.316kg左右 |
| D、以上说法均不对 |
 如图,已知两定点A(-6,0)和B(2,0),O为原点,若PO是△APB的内角平分线,求动点P的轨迹方程,并说明其轨迹表示什么图形.
如图,已知两定点A(-6,0)和B(2,0),O为原点,若PO是△APB的内角平分线,求动点P的轨迹方程,并说明其轨迹表示什么图形.