题目内容
已知数列an-an-1=2n-1,且a1=1.
(1)求a2,a3,a4;
(2)猜想出an并用数学归纳法证明.
(1)求a2,a3,a4;
(2)猜想出an并用数学归纳法证明.
考点:数学归纳法,数列递推式
专题:点列、递归数列与数学归纳法
分析:(1)由数列的递推关系an-an-1=2n-1,且a1=1,即可求得a2,a3,a4;
(2)由(1)可猜想:an=n2;再利用数学归纳法,分两步:①当n=1时,易证等式成立;②假设n=k时,命题成立,即ak=k2;去推证n=k+1时,等式也成立即可.
(2)由(1)可猜想:an=n2;再利用数学归纳法,分两步:①当n=1时,易证等式成立;②假设n=k时,命题成立,即ak=k2;去推证n=k+1时,等式也成立即可.
解答:
解:(1)∵an-an-1=2n-1,且a1=1,
∴a2=a1+2×2-1=1+2×2-1=4;
a3=a2+2×3-1=4+2×3-1=9,
同理可得:a4=16;
(2)由(1)可猜想:an=n2;
下面用数学归纳法证明:
①当n=1时,由已知a1=1=12,成立;
②假设n=k时,命题成立,即ak=k2;
则当n=k+1时,ak+1=ak+2(k+1)-1=k2+2k+1=(k+1)2,
即n=k+1时,等式也成立,
综合①②知,对?n∈N*,an=n2.
∴a2=a1+2×2-1=1+2×2-1=4;
a3=a2+2×3-1=4+2×3-1=9,
同理可得:a4=16;
(2)由(1)可猜想:an=n2;
下面用数学归纳法证明:
①当n=1时,由已知a1=1=12,成立;
②假设n=k时,命题成立,即ak=k2;
则当n=k+1时,ak+1=ak+2(k+1)-1=k2+2k+1=(k+1)2,
即n=k+1时,等式也成立,
综合①②知,对?n∈N*,an=n2.
点评:本题考查数列的递推关系及数学归纳法的应用,猜得an=n2是关键,考查运算及推理证明的能力,属于中档题.

练习册系列答案
 轻松课堂单元测试AB卷系列答案
轻松课堂单元测试AB卷系列答案 小题狂做系列答案
小题狂做系列答案
相关题目
下列哪组中的函数相等( )
A、y=x,y=(
| ||||||
B、y=
| ||||||
C、y=x2,y=
| ||||||
D、y=
|
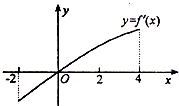 定义在[-2,+∞)的函数f(x)的部分值如下表,f(x)的导函数f(x)的图象如图,两正数a,b满足f(2a+b)<1,则
定义在[-2,+∞)的函数f(x)的部分值如下表,f(x)的导函数f(x)的图象如图,两正数a,b满足f(2a+b)<1,则| b+3 |
| a+3 |
A、(
| ||||
B、(
| ||||
C、(
| ||||
D、(-
|
为研究某大学女大学生的身高xcm和体重ykg的相关关系,据所抽取8名女生测得的数据可计算出线性回归方程为
=0.849x-85.712,由此方程知,当x=172(cm)时,y=60.316(kg),下列说法正确的是( )
 |
| y |
| A、身高为172cm的女大学生的体重是60.316kg |
| B、身高为172cm的所有女大学生的平均体重必为60.316kg |
| C、身高为172cm的女大学生的体重多数在60.316kg左右 |
| D、以上说法均不对 |