题目内容
已知幂函数f(x)=x-m2+m+2(m∈Z)在(0,+∞)上单调递增.
(1)求函数f(x)的解析式;
(2)设g(x)=f(x)-ax+1,a为实常数,求g(x)在区间[-1,1]上的最小值.
(1)求函数f(x)的解析式;
(2)设g(x)=f(x)-ax+1,a为实常数,求g(x)在区间[-1,1]上的最小值.
考点:二次函数在闭区间上的最值,函数解析式的求解及常用方法,二次函数的性质
专题:函数的性质及应用
分析:(1)由条件可得-m2+m+2>0,解得m的范围m.再结合m∈Z,求得m的值,可得f(x)的解析式.
(2)由(1)知g(x)=x2-ax+1,再分①若
≤-1、②若-1<
≤1、③若
>1三种情况,分别利用二次函数的性质,求得g(x)min..
(2)由(1)知g(x)=x2-ax+1,再分①若
| a |
| 2 |
| a |
| 2 |
| a |
| 2 |
解答:
解:(1)因为幂函数f(x)=x-m2+m+2 在(0,+∞)上单调递增,
所以-m2+m+2>0,故-1<m<2.
又因为m∈Z,故m=0,或m=1,所以f(x)=x2.
(2)由(1)知g(x)=x2-ax+1,
①若
≤-1,即a≤-2时,g(x)在[-1,1]上单调递增,
所以g(x)mi n=g(-1)=a+2.
②若-1<
≤1,即-2<a≤2时,
g(x)在[-1,
]上单调递减,[
,1]上单调递增,
所以g(x)min=g(
)=1-
.
③若
>1,即a>2时,g(x)在[-1,1]上单调递减,
所以g(x)min=g(1)=2-a.
综上:a≤-2时,g(x)在区间[-1,1]上的最小值为a+2;
-2<a≤2时,g(x)在区间[-1,1]上的最小值为1-
;
a>2时,g(x)在区间[-1,1]上的最小值为2-a.
所以-m2+m+2>0,故-1<m<2.
又因为m∈Z,故m=0,或m=1,所以f(x)=x2.
(2)由(1)知g(x)=x2-ax+1,
①若
| a |
| 2 |
所以g(x)mi n=g(-1)=a+2.
②若-1<
| a |
| 2 |
g(x)在[-1,
| a |
| 2 |
| a |
| 2 |
所以g(x)min=g(
| a |
| 2 |
| a2 |
| 4 |
③若
| a |
| 2 |
所以g(x)min=g(1)=2-a.
综上:a≤-2时,g(x)在区间[-1,1]上的最小值为a+2;
-2<a≤2时,g(x)在区间[-1,1]上的最小值为1-
| a2 |
| 4 |
a>2时,g(x)在区间[-1,1]上的最小值为2-a.
点评:本题主要考查幂函数额定义,求二次函数在闭区间上的最值,体现了分类讨论的数学思想,属于基础题.

练习册系列答案
相关题目
已知向量
、
,|
|=2,
=(3,4),
与
夹角等于30°,则
•
等于( )
| a |
| b |
| a |
| b |
| a |
| b |
| a |
| b |
| A、5 | ||||
B、
| ||||
C、5
| ||||
D、5
|
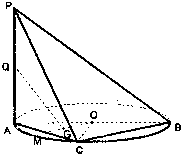 如图,AB是圆O的直径,PA垂直于圆O所在的平面,C是圆0上异于A,B的点,
如图,AB是圆O的直径,PA垂直于圆O所在的平面,C是圆0上异于A,B的点,