题目内容
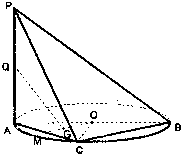 如图,AB是圆O的直径,PA垂直于圆O所在的平面,C是圆0上异于A,B的点,
如图,AB是圆O的直径,PA垂直于圆O所在的平面,C是圆0上异于A,B的点,(1)求证:BC⊥平面PAC;
(2)设Q,M分别为PA,AC的中点,问:对于线段OM上的任一点G,是否都有QG∥平面PBC?并说明理由.
考点:直线与平面垂直的判定,直线与平面平行的判定
专题:综合题,空间位置关系与距离
分析:(1)由PA⊥圆所在的平面,可得PA⊥BC,由直径对的圆周角等于90°,可得BC⊥AC,根据直线和平面垂直的判定定理可得结论.
(2)利用三角形的中位线性质,证明OM∥BC,QM∥PC,可得平面OQM∥平面PBC,从而证明QG∥平面PBC.
(2)利用三角形的中位线性质,证明OM∥BC,QM∥PC,可得平面OQM∥平面PBC,从而证明QG∥平面PBC.
解答:
(1)证明:因为PA⊥圆所在的平面ABC,BC?平面ABC,所以可得PA⊥BC,
因为C是圆O上的点,AB是圆O的直径,所以由直径对的圆周角等于90°,可得BC⊥AC.
再由AC∩PA=A,利用直线和平面垂直的判定定理可得BC⊥平面PAC;
(2)对于线段OM上的任一点G,都有QG∥平面PBC.证明如下:
连接QM,QO,则
因为Q,M分别为PA,AC的中点,所以QM∥BC,
因为QM?平面PBC,BC?平面PBC,所以QM∥平面PBC,
因为OM是△ABC的中位线,所以有OM∥BC,
因为OM?平面PBC,BC?平面PBC,所以OM∥平面PBC.
而OM和QM是平面OQM内的两条相交直线,故平面OQM∥平面PBC.
又QG?平面OQM,所以QG∥平面PBC.
因为C是圆O上的点,AB是圆O的直径,所以由直径对的圆周角等于90°,可得BC⊥AC.
再由AC∩PA=A,利用直线和平面垂直的判定定理可得BC⊥平面PAC;
(2)对于线段OM上的任一点G,都有QG∥平面PBC.证明如下:
连接QM,QO,则
因为Q,M分别为PA,AC的中点,所以QM∥BC,
因为QM?平面PBC,BC?平面PBC,所以QM∥平面PBC,
因为OM是△ABC的中位线,所以有OM∥BC,
因为OM?平面PBC,BC?平面PBC,所以OM∥平面PBC.
而OM和QM是平面OQM内的两条相交直线,故平面OQM∥平面PBC.
又QG?平面OQM,所以QG∥平面PBC.
点评:本题主要考查直线和平面垂直的判定定理、直线和平面平行的判定定理的应用,属于中档题.

练习册系列答案
相关题目
如图程序运行的结果是( )


| A、11 | B、13 | C、15 | D、17 |
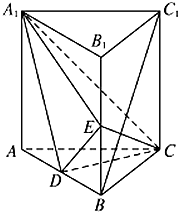 如图,直棱柱ABC-A1B1C1中,D,E分别是AB,BB1的中点,AA1=AC=CB=
如图,直棱柱ABC-A1B1C1中,D,E分别是AB,BB1的中点,AA1=AC=CB=