题目内容
已知抛物线y=ax2经过点(1,-
),则该抛物线的焦点坐标为( )
| 1 |
| 4 |
A、(0,-
| ||
B、(0,-
| ||
| C、(0,-1) | ||
| D、(0,1) |
考点:抛物线的简单性质
专题:圆锥曲线的定义、性质与方程
分析:把点(1,-
)代入抛物线方程可得a,进而求出抛物线的标准方程,结合抛物线的性质,进而得到焦点坐标.
| 1 |
| 4 |
解答:
解:∵抛物线y=ax2经过点(1,-
),
∴a=-
,
∴抛物线标准方程为x2=-4y,
∴抛物线焦点坐标为(0,-1).
故选:C.
| 1 |
| 4 |
∴a=-
| 1 |
| 4 |
∴抛物线标准方程为x2=-4y,
∴抛物线焦点坐标为(0,-1).
故选:C.
点评:本题考查了抛物线的标准方程及其性质,属于基础题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
设全集U=R,且A={x||x-1|>2},B={x|x2-6x+8<0},则(∁UA)∩B=( )
| A、[-1,4) |
| B、(2,3) |
| C、(2,3] |
| D、(-1,4) |
已知tanα=
,则
等于( )
| 1 |
| 2 |
| cos2α+sin2α+1 |
| cos2α |
| A、4 | ||
| B、6 | ||
| C、12 | ||
D、
|
已知数列{an}满足2an+1+an=0,a1=-2,则数列{an}的前10项和S10为( )
A、
| ||
B、
| ||
C、
| ||
D、
|
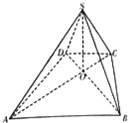 如图所示,四棱锥S-ABCD的底面ABCD为等腰梯形,AB∥CD,对角线AC与BD交于点O,OA=3,OD=1,CD=
如图所示,四棱锥S-ABCD的底面ABCD为等腰梯形,AB∥CD,对角线AC与BD交于点O,OA=3,OD=1,CD=