题目内容
从0,1,2,3,4,5,6,7,8,9,这10个数字中同时取4个不同的数,其和为偶数,则不同的取法为 (用数字作答).
考点:分步乘法计数原理
专题:排列组合
分析:分别求得取出的这4个数都是偶数;取出的这4个数都是奇数;取出的这4个数有2个是偶数、2个是奇数这三种情况的方法数,相加,即得所求.
解答:
解:若取出的这4个数都是偶数,方法有
=5种;
若取出的这4个数都是奇数,方法有
=5种;
若取出的这4个数有2个是偶数、2个是奇数,方法有
•
=100种.
综上,所有的满足条件的取法共有5+5+100=110种,
故答案为:110.
| C | 4 5 |
若取出的这4个数都是奇数,方法有
| C | 4 5 |
若取出的这4个数有2个是偶数、2个是奇数,方法有
| C | 2 5 |
| C | 2 5 |
综上,所有的满足条件的取法共有5+5+100=110种,
故答案为:110.
点评:本题主要考查分步计数原理的应用,体现了分类讨论的数学思想,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
已知函数f(x)的定义域为(-∞,+∞),如果f(x+2014)=
那么f(2014+
)•f(-7986)=( )
|
| π |
| 4 |
| A、2014 | ||
| B、4 | ||
C、
| ||
D、
|
已知双曲线
-
=1(a>0)的一条渐近线与圆(x-3)2+y2=8相交于M,N两点且|MN|=4,则此双曲线的离心率为( )
| x2 |
| a2 |
| y2 |
| 4 |
A、
| ||||
B、
| ||||
C、
| ||||
| D、5 |
已知f(x)为R上的可导函数,且?x∈R,均有f(x)>f′(x),则以下判断正确的是( )
| A、f(2013)>e2013f(0) |
| B、f(2013)<e2013f(0) |
| C、f(2013)=e2013f(0) |
| D、f(2013)与e2013f(0)大小无法确定 |
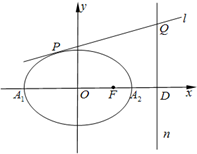 如图,已知椭圆
如图,已知椭圆