题目内容
根据三个函数f(x)=2x,g(x)=2x,h(x)=log2x给出以下五句话:
(1)f(x),g(x),h(x)在其定义域上都是增函数;
(2)f(x)的增长速度始终不变;
(3)f(x)的增长速度越来越快;
(4)g(x)的增长速度越来越快;
(5)h(x)的增长速度越来越慢.
其中正确的个数为( )
(1)f(x),g(x),h(x)在其定义域上都是增函数;
(2)f(x)的增长速度始终不变;
(3)f(x)的增长速度越来越快;
(4)g(x)的增长速度越来越快;
(5)h(x)的增长速度越来越慢.
其中正确的个数为( )
| A、2 | B、3 | C、4 | D、5 |
考点:命题的真假判断与应用
专题:函数的性质及应用,导数的综合应用
分析:(1)利用幂函数、指数函数及对数函数的单调性质即可判断其正误;
(2)f′(x)=2,利用导数的几何意义可知(2)与(3)的正误;
(4)利用g′(x)=2xin2为增函数,可判断(4)的正误;
(5)利用h′(x)=
>0,在(0,+∞)上为减函数,可判断(5)之正误.
(2)f′(x)=2,利用导数的几何意义可知(2)与(3)的正误;
(4)利用g′(x)=2xin2为增函数,可判断(4)的正误;
(5)利用h′(x)=
| 1 |
| xln2 |
解答:
解:∵f(x)=2x,g(x)=2x,h(x)=log2x,
∴f(x),g(x),h(x)在其定义域上都是增函数,即(1)正确;
又f′(x)=2,
∴f(x)的增长速度始终不变,即(2)正确,(3)错误;
∵g′(x)=2xin2为增函数,
∴g(x)的增长速度越来越快,即(4)正确;
又h′(x)=
>0,在(0,+∞)上为减函数,
∴h(x)的增长速度越来越慢,即(5)正确;
综上所述,正确的命题为:(1)(2)(4)(5),共4个.
故选:C.
∴f(x),g(x),h(x)在其定义域上都是增函数,即(1)正确;
又f′(x)=2,
∴f(x)的增长速度始终不变,即(2)正确,(3)错误;
∵g′(x)=2xin2为增函数,
∴g(x)的增长速度越来越快,即(4)正确;
又h′(x)=
| 1 |
| xln2 |
∴h(x)的增长速度越来越慢,即(5)正确;
综上所述,正确的命题为:(1)(2)(4)(5),共4个.
故选:C.
点评:本题考查命题的真假判断与应用,着重考查导数的几何意义及应用,属于中档题.

练习册系列答案
相关题目
某三棱锥的三视图如图所示,该三棱锥的体积是( )


A、18
| ||
B、36
| ||
C、12
| ||
D、24
|
若P是两条异面直线l,m外的任意一点,则下列命题:
①过点P有且只有一条直线与l,m都平行;
②过点P有且只有一条直线与l,m都垂直;
③过点P有且只有一条直线与l,m都相交;
④过点P有且只有一条直线与l,m都异面.
其中假命题的个数为( )
①过点P有且只有一条直线与l,m都平行;
②过点P有且只有一条直线与l,m都垂直;
③过点P有且只有一条直线与l,m都相交;
④过点P有且只有一条直线与l,m都异面.
其中假命题的个数为( )
| A、1 | B、2 | C、3 | D、4 |
已知i是虚数单位,若(m+i)2=3-4i,则实数m的值为( )
| A、-2 | ||
| B、±2 | ||
C、±
| ||
| D、2 |
一只蚂蚁在三边长分别为3,4,5的三角形内爬行,则此蚂蚁距离三角形三个顶点的距离均超过1的概率为( )
A、1-
| ||
B、1-
| ||
C、
| ||
D、
|
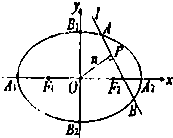 如图,椭圆C:
如图,椭圆C: