题目内容
已知f（x）为R上的可导函数，且?x∈R，均有f（x）＞f′（x），则以下判断正确的是（ ）
| A、f（2013）＞e2013f（0） |
| B、f（2013）＜e2013f（0） |
| C、f（2013）=e2013f（0） |
| D、f（2013）与e2013f（0）大小无法确定 |
考点：导数的运算
专题：函数的性质及应用
分析：设函数h（x）=
，求得h′（x）＜0，可得h（x）在R上单调递减，可得h（2013）＜h（0），再进一步化简，可得结论．
| f(x) |
| ex |
解答：
解：设函数h（x）=
，
∵?x∈R，均有f（x）＞f′（x），则h′（x）=
＜0，
∴h（x）在R上单调递减，∴h（2013）＜h（0），即
＜
，
即 f（2013）＜e2013f（0），
故选：B．
| f(x) |
| ex |
∵?x∈R，均有f（x）＞f′（x），则h′（x）=
| f′(x)•ex-f(x)•ex |
| (ex)2 |
∴h（x）在R上单调递减，∴h（2013）＜h（0），即
| f(2013) |
| e2013 |
| f(0) |
| e0 |
即 f（2013）＜e2013f（0），
故选：B．
点评：本题主要考查利用导数研究函数的单调性，利用函数的单调性比较两个函数值的大小，属于基础题．
练习册系列答案
每课必练系列答案
巧学巧练系列答案
相关题目
如图，设椭圆C：已知i是虚数单位，若（m+i）2=3-4i，则实数m的值为（ ）
| A、-2 | ||
| B、±2 | ||
C、±
| ||
| D、2 |
一只蚂蚁在三边长分别为3，4，5的三角形内爬行，则此蚂蚁距离三角形三个顶点的距离均超过1的概率为（ ）
A、1-
| ||
B、1-
| ||
C、
| ||
D、
|
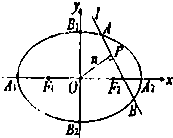如图，椭圆C：