题目内容
8.已知四面体ABCD的四个顶点都在球O的表面上,AB⊥平面BCD,又AB=3,BC=2,BD=4,且∠CBD=60°,则球O的表面积为( )| A. | 12π | B. | 16π | C. | 20π | D. | 25π |
分析 由余弦定理求出CD=2$\sqrt{3}$,以AB、BC、CD、AB为长方体的长、宽、高构造长方体AGHF-BCDF,球O的半径R=$\frac{1}{2}EC$,由此能求出球O的表面积.
解答 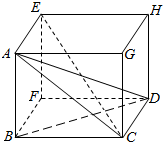 解:∵四面体ABCD的四个顶点都在球O的表面上,AB⊥平面BCD,
解:∵四面体ABCD的四个顶点都在球O的表面上,AB⊥平面BCD,
又AB=3,BC=2,BD=4,且∠CBD=60°,
∴CD=$\sqrt{16+4-2×4×2×cos60°}$=2$\sqrt{3}$,
∴BC2+CD2=BD2,∴AB⊥平面BCD,BC⊥CD,
∴以AB、BC、CD、AB为长方体的长、宽、高构造长方体AGHF-BCDF,
则球O的半径R=$\frac{1}{2}EC$=$\frac{1}{2}\sqrt{9+4+12}$=$\frac{5}{2}$,
∴球O的表面积S=4$π×(\frac{5}{2})^{2}$=25π.
故选:D.
点评 本题考查球的表面积的求法,是中档题,解题时要认真审题,注意构造法的合理运用.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
18.某四棱锥的三视图如图所示,该四棱锥的体积是( )


| A. | 32 | B. | $\frac{32}{3}$ | C. | 48 | D. | $\frac{16}{3}$ |
19.在矩形ABCD中,AB=$\sqrt{5}$,BC=$\sqrt{3}$,P为矩形内一点,且AP=$\frac{\sqrt{5}}{2}$,若$\overrightarrow{AP}$=λ$\overrightarrow{AB}$+μ$\overrightarrow{AD}$(λ,μ∈R),则$\sqrt{5}$λ+$\sqrt{3}$μ的最大值为( )
| A. | $\frac{\sqrt{5}}{2}$ | B. | $\frac{\sqrt{10}}{2}$ | C. | $\frac{3+\sqrt{3}}{4}$ | D. | $\frac{\sqrt{6}+3\sqrt{2}}{4}$ |
16.已知集合A={0,1},B={z|z=x+y,x∈A,y∈A},则B的子集个数为( )
| A. | 3 | B. | 4 | C. | 7 | D. | 8 |