题目内容

求下列函数的值域：y=
2x-1
3x+2
．
考点：函数的值域
专题：函数的性质及应用
分析：利用分离常数法，可将原函数的解析式化为y=
2
3
-
7
3
3x+2
，进而根据
7
3
3x+2
≠0，可得y≠
2
3
，进而得到函数的值域．
解答： 解：∵y=
2x-1
3x+2
=
2
3
(3x+2)-
7
3
3x+2
=
2
3
-
7
3
3x+2
，
∵
7
3
3x+2
≠0，故y≠
2
3
，
故函数y=
2x-1
3x+2
的值域为：{y|y≠
2
3
}，
点评：本题考查的知识点是函数的值域，熟练掌握求函数值域的方法--分离常数法，是解答的关键．
练习册系列答案
相关题目
若空间中四条两两不同的直线l1，l2，l3，l4，满足l1⊥l2，l2∥l3，l3⊥l4，则下列结论一定正确的是（　　）
A、l1⊥l4
B、l1∥l4
C、l1与l4既不垂直也不平行
D、l1与l4的位置关系不确定
设数列{an}的前n项和为Sn，满足Sn=2nan+1-3n2-4n，n∈N*，且S3=15．
（1）求a1，a2，a3的值；
（2）求数列{an}的通项公式．
已知函数f（x）=x-
a
x
（a＞0），g（x）=2lnx．
（1）若对[1，+∞）内任意的x，不等式f（x）≥g（x）恒成立，求a的取值范围；
（2）当a=1时，
（i）．求最大正整数k，使得任意k个实数x1，x2，…，xk∈[e，3]，都有f（x1）+f（x2）+…+f（xk-1）≤16g（xk）成立（e=2.71828…是自然对数的底数）；
（ii）．求证：
n
i=1
4i
4i2-1
＞ln（2n+1）（i，n∈N*）．
已知函数f（x）=sin（3x+
π
4
）．
（1）求f（x）的单调递增区间；
（2）若α是第二象限角，f（
α
3
）=
4
5
cos（α+
π
4
）cos2α，求cosα-sinα的值．
设△ABC的内角A，B，C所对边的长分别为a，b，c，且b=3，c=1，△ABC的面积为
2
，求cosA与a的值．
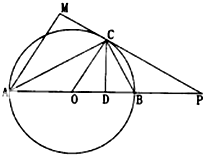如图，已知AB是⊙O的直径，C为⊙O上一点，以C为切点的切线交AB的延长线于点P，AM⊥CP，垂足为M，CD⊥AB，垂足为D．
（1）求证：AD=AM；
（2）若⊙O的直径为2，∠PCB=30°，求PC的长．
已知复数z=（5+2i）2（i为虚数单位），则z的实部为
 
．
若将函数f（x）=sin（2x+
π
4
）的图象向右平移φ个单位，所得图象关于y轴对称，则φ的最小正值是
 
．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网