题目内容
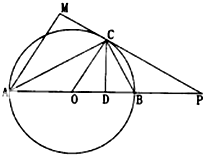 如图,已知AB是⊙O的直径,C为⊙O上一点,以C为切点的切线交AB的延长线于点P,AM⊥CP,垂足为M,CD⊥AB,垂足为D.
如图,已知AB是⊙O的直径,C为⊙O上一点,以C为切点的切线交AB的延长线于点P,AM⊥CP,垂足为M,CD⊥AB,垂足为D.(1)求证:AD=AM;
(2)若⊙O的直径为2,∠PCB=30°,求PC的长.
考点:与圆有关的比例线段
专题:选作题,立体几何
分析:(1)通过证明△AMC≌△ADC,可得AD=AM;
(2)计算出PB,再利用切割线定理,求PC的长.
(2)计算出PB,再利用切割线定理,求PC的长.
解答:
(1)证明:∵AB是⊙O的直径,
∴∠ACB=90°,
∴∠ACD+∠BCD=90°,
∵CD⊥AB,
∴∠ABC+∠BCD=90°,
∴∠ACD=∠ABC,
∵以C为切点的切线交AB的延长线于点P,
∴∠MCA=∠ABC=∠ACD,
∵∠AMC=∠ADC=90°,AC=AC,
∴△AMC≌△ADC,
∴AD=AM;
(2)解:∵∠PCB=30°,以C为切点的切线交AB的延长线于点P,
∴∠PAC=∠PCB=30°,
在Rt△ABC中,AB=2,∠BAC=30°,
∴BC=1,∠ABC=60°,
∴∠BPC=30°,
∴∠BPC=∠BCP,BC=BP=1,
由切割线定理得PC2=PB•PA=PB(PB+BA)=3,
∴PC=
.
∴∠ACB=90°,
∴∠ACD+∠BCD=90°,
∵CD⊥AB,
∴∠ABC+∠BCD=90°,
∴∠ACD=∠ABC,
∵以C为切点的切线交AB的延长线于点P,
∴∠MCA=∠ABC=∠ACD,
∵∠AMC=∠ADC=90°,AC=AC,
∴△AMC≌△ADC,
∴AD=AM;
(2)解:∵∠PCB=30°,以C为切点的切线交AB的延长线于点P,
∴∠PAC=∠PCB=30°,
在Rt△ABC中,AB=2,∠BAC=30°,
∴BC=1,∠ABC=60°,
∴∠BPC=30°,
∴∠BPC=∠BCP,BC=BP=1,
由切割线定理得PC2=PB•PA=PB(PB+BA)=3,
∴PC=
| 3 |
点评:本题考查三角形全等的证明,考查切割线定理,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
相关题目
若变量x,y满足约束条件
,则z=2x+y的最大值等于( )
|
| A、7 | B、8 | C、10 | D、11 |