题目内容
5.设点M(x0,1),设在圆O:x2+y2=1上存在点N,使得∠OMN=30°,则实数x0的取值范围为$[-\sqrt{3},\sqrt{3}]$.分析 易知M点在直线y=1上,若设圆x2+y2=1与直线y=1的交点为T,显然假设存在点N,使得∠OMN=30°,则必有∠OMN≤∠OMT,所以只需∠OMT≥30°即可,借助于三角函数容易求出x0的范围.
解答 解:易知M(x0,1)在直线y=1上,设圆x2+y2=1与直线y=1的交点为T,显然假设存在点N,使得∠OMN=30°,则必有∠OMN≤∠OMT,
所以要是圆上存在点N,使得∠OMN=30°,只需∠OMT≥30°,
因为T(0,1),所以只需在Rt△OMT中,tan∠OMT=$\frac{1}{|{x}_{0}|}$≥tan30°=$\frac{1}{\sqrt{3}}$,
当x0=0时,显然满足题意,
故x0∈$[-\sqrt{3},\sqrt{3}]$.
故答案为$[-\sqrt{3},\sqrt{3}]$.
点评 此题重点考查了利用数形结合的思想方法解题,关键是弄清楚M点所在的位置,能够找到∠OMN与∠OMT的大小关系,从而构造出关于x0的不等式.

练习册系列答案
相关题目
13.将数30012(4)转化为十进制数为( )
| A. | 524 | B. | 260 | C. | 256 | D. | 774 |
20.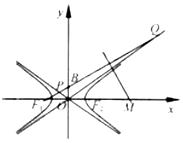 如图,F1,F2分别是双曲线C:$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1$(a,b>0)的左、右焦点,B是虚轴的端点,直线F1B与C的两条渐近线分别交于P,Q两点,线段PQ的垂直平分线与x轴交于点M,若|MF2|=|F1F2|,则双曲线C的渐近线方程是( )
如图,F1,F2分别是双曲线C:$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1$(a,b>0)的左、右焦点,B是虚轴的端点,直线F1B与C的两条渐近线分别交于P,Q两点,线段PQ的垂直平分线与x轴交于点M,若|MF2|=|F1F2|,则双曲线C的渐近线方程是( )
 如图,F1,F2分别是双曲线C:$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1$(a,b>0)的左、右焦点,B是虚轴的端点,直线F1B与C的两条渐近线分别交于P,Q两点,线段PQ的垂直平分线与x轴交于点M,若|MF2|=|F1F2|,则双曲线C的渐近线方程是( )
如图,F1,F2分别是双曲线C:$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1$(a,b>0)的左、右焦点,B是虚轴的端点,直线F1B与C的两条渐近线分别交于P,Q两点,线段PQ的垂直平分线与x轴交于点M,若|MF2|=|F1F2|,则双曲线C的渐近线方程是( )| A. | y=±x | B. | $y=±\sqrt{3}x$ | C. | $y=±\frac{1}{2}x$ | D. | $y=±\frac{{\sqrt{2}}}{2}x$ |
10.若实数a,b,c满足loga3<logb3<logc3,则下列关系中不可能成立的( )
| A. | a<b<c | B. | b<a<c | C. | c<b<a | D. | a<c<b |
15.已知三棱锥P-ABC的三条侧棱PA、PB、PC两两互相垂直,且PA=2,PB=$\sqrt{3}$,PC=3,则这个三棱锥的外接球的表面积为( )
| A. | 16π | B. | 32π | C. | 36π | D. | 64π |
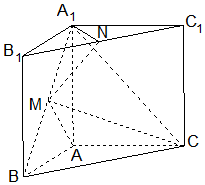 在三棱柱ABC-A1B1C1中,侧棱与底面垂直,∠BAC=90°,AB=AA1,点M,N分别为A1B 和B1C1的中点.
在三棱柱ABC-A1B1C1中,侧棱与底面垂直,∠BAC=90°,AB=AA1,点M,N分别为A1B 和B1C1的中点.