题目内容
8．已知sinx+cosx=$\frac{1}{5}$（0≤x＜π），则tanx的值等于（ ）| A． | -$\frac{3}{4}$ | B． | -$\frac{4}{3}$ | C． | $\frac{3}{4}$ | D． | $\frac{4}{3}$ |
分析 先根据sinx+cosx的值和二者的平方关系联立求得cosx的值，进而根据同角三角函数的基本关系求得sinx的值，最后利用商数关系求得tanx的值．
解答 解：由sinx+cosx=$\frac{1}{5}$，得sinx=$\frac{1}{5}$-cosx，代入sin2x+cos2x=1，
得：（5cosx-4）（5cosx+3）=0，
∴cosx=$\frac{4}{5}$或cosx=-$\frac{3}{5}$，当cosx=$\frac{4}{5}$时，得sinx=-$\frac{3}{5}$，
又∵0≤x＜π，
∴sinx≥0，故这组解舍去；
∴当cosx=-$\frac{3}{5}$时，sinx=$\frac{4}{5}$，tanx=-$\frac{4}{3}$．
故选：B．
点评 本题主要考查了同角三角函数的基本关系的应用．解题的过程中要特别注意根据角的范围确定三角函数值的正负号，考查了计算能力和转化思想，属于基础题．
练习册系列答案
阅读快车系列答案
相关题目
3．
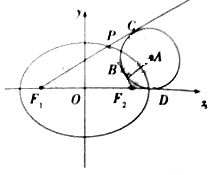如图，F1，F2分别是椭圆$\frac{{x}^{2}}{4}$+$\frac{{y}^{2}}{{b}^{2}}$=1（b＞0）的左，右焦点，椭圆的离心率为$\sqrt{3}$-1，P为椭圆上第一象限内的一点，$\overrightarrow{P{F}_{1}}$•$\overrightarrow{P{F}_{2}}$=0，圆A与△PF1F2三边所在直线都相切，切点分别为B，C，D，则圆A的半径为（ ）
如图，F1，F2分别是椭圆$\frac{{x}^{2}}{4}$+$\frac{{y}^{2}}{{b}^{2}}$=1（b＞0）的左，右焦点，椭圆的离心率为$\sqrt{3}$-1，P为椭圆上第一象限内的一点，$\overrightarrow{P{F}_{1}}$•$\overrightarrow{P{F}_{2}}$=0，圆A与△PF1F2三边所在直线都相切，切点分别为B，C，D，则圆A的半径为（ ）| A． | 4$\sqrt{3}$ | B． | 4$\sqrt{3}$-6 | C． | 4$\sqrt{3}$-2 | D． | 6-2$\sqrt{3}$ |
13．将数30012（4）转化为十进制数为（ ）
| A． | 524 | B． | 260 | C． | 256 | D． | 774 |
20．
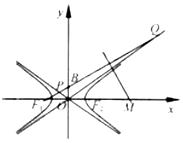如图，F1，F2分别是双曲线C：$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1$（a，b＞0）的左、右焦点，B是虚轴的端点，直线F1B与C的两条渐近线分别交于P，Q两点，线段PQ的垂直平分线与x轴交于点M，若|MF2|=|F1F2|，则双曲线C的渐近线方程是（ ）
如图，F1，F2分别是双曲线C：$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1$（a，b＞0）的左、右焦点，B是虚轴的端点，直线F1B与C的两条渐近线分别交于P，Q两点，线段PQ的垂直平分线与x轴交于点M，若|MF2|=|F1F2|，则双曲线C的渐近线方程是（ ）| A． | y=±x | B． | $y=±\sqrt{3}x$ | C． | $y=±\frac{1}{2}x$ | D． | $y=±\frac{{\sqrt{2}}}{2}x$ |
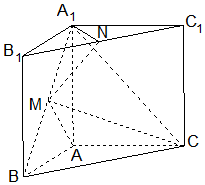在三棱柱ABC-A1B1C1中，侧棱与底面垂直，∠BAC=90°，AB=AA1，点M，N分别为A1B 和B1C1的中点．