题目内容
5.在调查男女乘客是否晕机的情况中,已知男乘客晕机为28人,不会晕机的也是28人,而女乘客晕机为28人,不会晕机的为56人.| 晕机 | 不晕机 | 总计 | |
| 男乘客 | |||
| 女乘客 | |||
| 总计 |
(2)试判断晕机是否与性别有关?
(参考数据:K2≥2.706时,有90%的把握判定变量A,B有关联;K2≥3.841时,有95%的把握判定变量A,B有关联;K2≥6.635时,有99%的把握判定变量A,B有关联.参考公式:${K^2}=\frac{{n{{(ad-bc)}^2}}}{(a+c)(b+d)(a+b)(c+d)}$)
分析 (1)根据题意,填写列联表即可;
(2)根据表中数据,计算观测值K2,对照临界值即可得出结论.
解答 解:(1)根据题意,填写列联表如下;
| 晕机 | 不晕机 | 总计 | |
| 男乘客 | 28 | 28 | 56 |
| 女乘客 | 28 | 56 | 84 |
| 总计 | 56 | 84 | 140 |
=$\frac{140{×(28×56-28×28)}^{2}}{56×84×56×84}$≈3.889≥3.841,
对照临界值知,有95%的把握判定变量A,B有关联.
点评 本题考查了独立性检验的应用问题,是基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
13.点P(x,y)在$\left\{\begin{array}{l}{x=2+2cosθ}\\{y=1+sinθ}\end{array}\right.$(θ为参数)上,则x+y的最大值为( )
| A. | 3+$\sqrt{5}$ | B. | 5+$\sqrt{5}$ | C. | 5 | D. | 6 |
20.从装有两个红球和两个黑球的口袋里任取两个球,那么对立的两个事件是( )
| A. | “至少有一个黑球”与“都是黑球” | |
| B. | “至少有一个黑球”与“至少有一个红球” | |
| C. | “恰好有一个黑球”与“恰好有两个黑球” | |
| D. | “至少有一个黑球”与“都是红球” |
14.已知$|{\vec b}|=3$,$\vec a$在$\vec b$方向上的投影为$\frac{3}{2}$,则$\vec a$•$\vec b$=( )
| A. | 2 | B. | $\frac{9}{2}$ | C. | 2 | D. | $\frac{1}{2}$ |
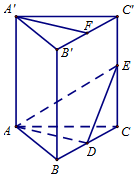 如图,在直三棱柱ABC-A'B'C'中,AB=AC,D、E分别是棱BC、CC'上的点(点D不同于点C),且AD⊥BC,F为B'C'的中点.求证:
如图,在直三棱柱ABC-A'B'C'中,AB=AC,D、E分别是棱BC、CC'上的点(点D不同于点C),且AD⊥BC,F为B'C'的中点.求证: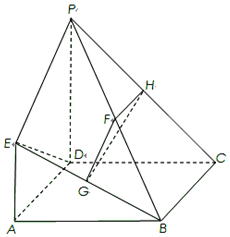 如图,已知四边形ABCD是正方形,EA⊥平面ABCD,PD∥EA,AD=PD=2EA=2,F,G,H分别为BP,BE,PC的中点.
如图,已知四边形ABCD是正方形,EA⊥平面ABCD,PD∥EA,AD=PD=2EA=2,F,G,H分别为BP,BE,PC的中点.