题目内容
设函数f(x)=x2-ax+b,a,b∈R.
(1)已知f(x)在区间(-∞,1)上单调递减,求a的取值范围;
(2)存在实数a,使得当x∈[0,b]时,2≤f(x)≤6恒成立,求b的最大值及此时a的值.
(1)已知f(x)在区间(-∞,1)上单调递减,求a的取值范围;
(2)存在实数a,使得当x∈[0,b]时,2≤f(x)≤6恒成立,求b的最大值及此时a的值.
考点:函数恒成立问题,二次函数的性质
专题:函数的性质及应用
分析:(1)利用对称轴和单调区间的关系,即可求a的取值范围;
(2)根据不等式恒成立,转化为求相应的最值即可.
(2)根据不等式恒成立,转化为求相应的最值即可.
解答:
解:(1)∵函数的对称轴为x=
,
∴要使f(x)在区间(-∞,1)上单调递减,则满足对称轴x=
≥1,即a≥2.
(2)∵当x∈[0,b]时,2≤f(x)≤6恒成立,
∴b>0,
①若a≤0,则
≤1,此时f(x)在[0,b]上单调递增,
∴
,即
,
由b2-ab+b≤6得a≥b-
+1≥2-
+1=0,
∴a=0,此时
,
解得
.
②若0<
<
,即0<a<b,此时
,
即
,∴
,即
,
∴2<b<6,
又b-
≥2,则a≤2
,
∴b-
+1≤2
,
令h(x)=x-
+1,g(x)=2
,
∴h(2)=g(2)=0,h(3)=g(3)=2,且h(x)与g(x)均在(2,6)上单调递增,
当2<x<3时,h(x)的图象在g(x)图象的下方,即此时h(x)<g(x),
∴不等式b-
+1≤2
的解为2<b≤3,
当b=3时,
,即
,解得a=2.
③若0<
=
,即0<a=b,此时
,
即
,此时不等式无解.
④若0<
<
<b,即0<b<a<2b,此时
,即
,
即
,∴
+2<a,a2-4a+8<0此时不等式无解.
⑤若
≥b,即a≥2b,此时f(x)在[0,b]上单调递减,
∴
,即
,即
,
∴2b≤b-
+1,
即b+
≤1,而当b>0时,b+
≥2
>1,∴此时不等式无解.
综上b的取值范围是[2,3],b的最大值是3,此时a=2.
| a |
| 2 |
∴要使f(x)在区间(-∞,1)上单调递减,则满足对称轴x=
| a |
| 2 |
(2)∵当x∈[0,b]时,2≤f(x)≤6恒成立,
∴b>0,
①若a≤0,则
| a |
| 2 |
∴
|
|
由b2-ab+b≤6得a≥b-
| 6 |
| b |
| 6 |
| 2 |
∴a=0,此时
|
解得
|
②若0<
| a |
| 2 |
| b |
| 2 |
|
即
|
|
|
∴2<b<6,
又b-
| a2 |
| 4 |
| b-2 |
∴b-
| 6 |
| b |
| b-2 |
令h(x)=x-
| 6 |
| x |
| x-2 |
∴h(2)=g(2)=0,h(3)=g(3)=2,且h(x)与g(x)均在(2,6)上单调递增,
当2<x<3时,h(x)的图象在g(x)图象的下方,即此时h(x)<g(x),
∴不等式b-
| 6 |
| b |
| b-2 |
当b=3时,
|
|
③若0<
| a |
| 2 |
| b |
| 2 |
|
即
|
④若0<
| b |
| 2 |
| a |
| 2 |
|
|
即
|
| a2 |
| 4 |
⑤若
| a |
| 2 |
∴
|
|
|
∴2b≤b-
| 2 |
| b |
即b+
| 2 |
| b |
| 2 |
| b |
| 2 |
综上b的取值范围是[2,3],b的最大值是3,此时a=2.
点评:本题主要考查二次函数的图象和性质,综合性较强,运算量较大,难度不小.

练习册系列答案
 新课标快乐提优暑假作业陕西旅游出版社系列答案
新课标快乐提优暑假作业陕西旅游出版社系列答案 暑假衔接培优教材浙江工商大学出版社系列答案
暑假衔接培优教材浙江工商大学出版社系列答案 欣语文化快乐暑假沈阳出版社系列答案
欣语文化快乐暑假沈阳出版社系列答案
相关题目
某社区四支篮球队参加比赛,现任意将这四支队分成两个组(每组两个队)进行比赛,胜者再赛,则所有可能的比赛情况共有( )
| A、3种 | B、6种 |
| C、12种 | D、24种 |
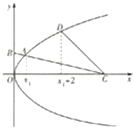 抛物线M:y2=2px(p>0)的准线过椭圆N:
抛物线M:y2=2px(p>0)的准线过椭圆N: